queenspublic
- 59
- 0
1. Problem
A spring with a pointer attached is hanging next to a scale marked in millimeters. Three different packages are hung from the spring, in turn, as shown below.
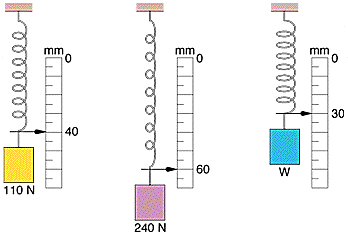
(a) Which mark on the scale will the pointer indicate when no package is hung from the spring?
(a) ? mm
(b) What is the weight W of the third package?
(b) ? N
2. Attempt at a solution
240 N - 110 N = 130 N
60 mm - 40 mm = 20 mm
130 N = -k * 20 mm <-- Is this formula correct? If not, how do I find the answers to (a) and (b)?
k = -6.5
A spring with a pointer attached is hanging next to a scale marked in millimeters. Three different packages are hung from the spring, in turn, as shown below.
(a) Which mark on the scale will the pointer indicate when no package is hung from the spring?
(a) ? mm
(b) What is the weight W of the third package?
(b) ? N
2. Attempt at a solution
240 N - 110 N = 130 N
60 mm - 40 mm = 20 mm
130 N = -k * 20 mm <-- Is this formula correct? If not, how do I find the answers to (a) and (b)?
k = -6.5
Attachments
Last edited: