hmvince
- 44
- 0
Homework Statement
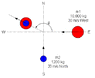
A mass(1) of 10000kg with a velocity 30m/s west collides with another mass(2) of 1200kg with a velocity 20m/s north. After the collision the two masses stick together. Determine the change in momentum of mass(2) before and after the collision.
Homework Equations
General momentum equations:
p = mv
Δp = pf - pi
The Attempt at a Solution
pi (mass 2) = mv = 1200 * 20 = 24000sN North
final velocity was calculated to be 26.87m/s 274.6°T (using LCM and some trig)
Therefore, pf (mass 2) = 1200 * 26.87 = 32244sN 274.6°T
to calculate change in momentum:
Δp = pf - pi
Δp = (32244sN 274.6°T) + (24000sN South)Note, changed to from North to south as it was -pi
Using a vector diagram, I found the resultant vector, Δp, to be 38621sN 226.7°T.I am not sure that I am doing this right though. After some searching on the internet, some people calculated change in momentum by adding initial and final vectors. But isn't that just net momentum?
please help!