How Do You Calculate the Design Angle θ for Strut AB in Vector Problems?

[Rybka]

Homework Statement

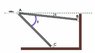
"Determine the design angle θ (0° ≤ θ ≤ 90°) for strut AB so that the 400-lb horizontal force has a component of 500lb directed from A towards C. What is the component of force acting along member AB? Take ϕ = 40°"

Homework Equations

x-component: magnitude*cos(θ)
y-component: magnitude*sin(θ)

The Attempt at a Solution

I understand what is being asked, I'm just unsure as to how I would get that AC component with what is given.

-Rybka

 

[NascentOxygen]

Hi Rybka. http://img96.imageshack.us/img96/5725/red5e5etimes5e5e45e5e25.gif

Take ϕ = 40°

Please correct this.

You have 3 forces, they must form a closed triangle. Struts exert their force in line with their length, so this tells you the directions of their contributions.

Are you given the correct answer?

 

[Rybka]

Good evening!

The solution is: θ = 53.5°, ForceAB = 621lb

 

[Rybka]

I figured it out.

The position of the struts in the first diagram is confusing, but the fact that we're solving for θ means their shape is variable.

Once I moved things around a little bit, it all became clear.

 

[NascentOxygen]

The solution is: θ = 53.5°, ForceAB = 621lb

It's always useful to know the answer. I was hoping you'd edit your post so it tells us exactly what is 40°. That would be useful for someone following along.

Good to know you worked it out.

 

[Al_muhnnak]

The problem in the drawing does not give accurate dimensions