How Do You Calculate the Initial Speed and Angle of a Projectile?

[maff is tuff]

Homework Statement

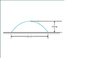
During a testing program, a photograph of the path of a projectile is taken, and subsequent measurements are added to the photo (See my attachment below .) Use the information shown in the figure to find

a) the initial speed of the projectile

b) the angle at which the projectile is fired

c) the time during which this projectile is in the air

Homework Equations

v = v0 + at

x-x0 = v0t + (1/2)at^2

v^2 = v0^2 + 2a(x-x0)

The Attempt at a Solution

I know the total x distance traveled is 25 m. So (x-x0) = 25
I also know that v(sub y) is 0 when the height is 4.9 m off the ground.
It also looks like y is 4.9 when x is 12.5. (but that's just an assumption so probably wrong)
If that were true then v(sub y) would be 0 when x is 12.5

I'm just having a hard time finding initial velocity.

If I plug in what I know I get stuck

25 = v0t

Or if I use the fact that v_y= 0 when y=4.9

4.9= 0 + v0y (1/2)(-9.8)t^2
t^2 = -1/v0_y which can't be right because something squared can't be negative

I'd really appreciate some help; I feel completely lost. Thanks

 

[gneill]

Your attachment isn't. Isn't attached, that is.

 

[maff is tuff]

oops sorry I thought I attached it. I will attach it now

 

[maff is tuff]

Ok it is attached. Sorry about that

 

[gneill]

y = y_o + vy*t - (1/2)*g*t²

Don't forget to multiply the initial velocity by time! That's why you're getting strange negative values under the radical.

 

[maff is tuff]

Oh ok that was the problem. Thanks, I keep overlooking these stupid errors.