- #1
SayedD
- 3
- 0
- Homework Statement
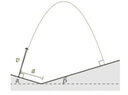
- A particle is shot perpendicular to respect to the inclined plane with inclination α, with initial velocity v. Determine the value of v so that the following particle hit the incline plane with inclination β perpendiculrly. The distance between the lowest point to the launching point is a.
I have been struggling all day trying to solve this by using a method which involves tilting the ground so it makes an inclined plane with inclination α+β, here are my steps
- Relevant Equations
- Given in my attempt
So using the projectile equation I got ##a\sin (\alpha + \beta) = v\sin (\alpha + \beta)t + \frac{g\sin \beta t^2}{2}##
To find t we use the other projectile equation:
Since the horizontal velocity must be 0 for it to hit the ground perpendicularly we set the equation to be:
##0 = v\sin (\alpha + \beta) - g\sin \beta t## \\
##t = \frac{v\sin (\alpha + \beta)}{g\sin \beta}##
please help solve using this method
To find t we use the other projectile equation:
Since the horizontal velocity must be 0 for it to hit the ground perpendicularly we set the equation to be:
##0 = v\sin (\alpha + \beta) - g\sin \beta t## \\
##t = \frac{v\sin (\alpha + \beta)}{g\sin \beta}##
please help solve using this method
Attachments
Last edited: