wilsonaj4
- 11
- 2
First off, I'm glad I'm finally a member on this board. It has helped me TREMENDOUSLY over the past few years with various problems I've had. You guys/gals are awesome and hopefully I can make some contributions to this site.
1. Homework Statement
A. Write down the partition function for positronium, assuming that only the levels illustrated in the diagram exist. Evaluate the partition function for T=20000K. Remember to include the degeneracies for each level. (I couldn't figure out how to copy and paste the diagram I was given, so I googled the one below. It's the same diagram, but the diagram I was given stops at the N=3 energy level)
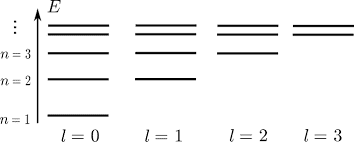
B. Write down an expression for the probability that the atom will exist in the state given by N=3, l=1, and determine that probability for T=20000K
C. Find an expression for the mean energy and evaluate that expression for T=20000K
1. En = 6.803eV (1 - 1/n2)
2. Z= ∑e-E(s)/KT
3. P(s)= 1/z * e-En/KT
4. ∑ E(s)* P(s)
A. So, we haven't done anything even close to this in class, so I'm a little coonfused, but to start, I substituted eq1 into the partition function in eq2 to get Z= ∑e-6.803eV (1 - 1/n2)/KT. After this, I'm completely stuck because we didn't really cover degeneracy in class very well. I know I'm supposed to multiply the expression by the degeneracy, but I'm not exactly sure how to do that.
B. Once A is found, this should be straightforward
C. Once A is found, this should be straightforwardMy work is due by 11/25 at 5pm (EST), any help would be greatly appreciated!
1. Homework Statement
A. Write down the partition function for positronium, assuming that only the levels illustrated in the diagram exist. Evaluate the partition function for T=20000K. Remember to include the degeneracies for each level. (I couldn't figure out how to copy and paste the diagram I was given, so I googled the one below. It's the same diagram, but the diagram I was given stops at the N=3 energy level)
B. Write down an expression for the probability that the atom will exist in the state given by N=3, l=1, and determine that probability for T=20000K
C. Find an expression for the mean energy and evaluate that expression for T=20000K
Homework Equations
1. En = 6.803eV (1 - 1/n2)
2. Z= ∑e-E(s)/KT
3. P(s)= 1/z * e-En/KT
4. ∑ E(s)* P(s)
The Attempt at a Solution
A. So, we haven't done anything even close to this in class, so I'm a little coonfused, but to start, I substituted eq1 into the partition function in eq2 to get Z= ∑e-6.803eV (1 - 1/n2)/KT. After this, I'm completely stuck because we didn't really cover degeneracy in class very well. I know I'm supposed to multiply the expression by the degeneracy, but I'm not exactly sure how to do that.
B. Once A is found, this should be straightforward
C. Once A is found, this should be straightforwardMy work is due by 11/25 at 5pm (EST), any help would be greatly appreciated!
Last edited: