How Do You Calculate the Period of a Transverse Wave on a Flexible String?

AI Thread Summary
To calculate the period of a transverse wave on a flexible string, first determine the mass density by converting the mass of the string to kilograms and dividing by its length. The velocity of the wave can be found using the formula V^2 = T/ρ, where T is the tension and ρ is the mass density. Once the velocity is known, the fundamental frequency can be calculated using the relationship v = f * λ, where λ is the wavelength. The period of the wave is then the inverse of the frequency. This method provides a systematic approach to solving the problem of wave oscillation on a string.
Tensionfreek
Messages
3
Reaction score
0
Transverse Wave on Flexible String! Please help.

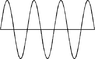
1. The diagram represents a snapshot of a standing transverse wave on a flexible string taken when the displacement is at a maximum. The string is 0.65 m long with tension 11.00 N. The total mass of the string is 8.11 g. Find the period of the oscillation.



2. converted mass to kg so .00811 kg Tension = 11N and L=0.65 m





3. i computed λ=2L/4 = 2(.65)/4 = .325 m

my v=f*λ which is the part i am currently stuck on because i cannot seem to figure out how to determine the fundamental frequency of a string without knowing the velocity first...
 

Attachments

  • prob19_stand8.gif
    prob19_stand8.gif
    2.8 KB · Views: 9,671
Physics news on Phys.org


i need an answer by at least 1130PM tonight! i have been trying this problem for hours and still have nothing...
 


See,

http://en.wikipedia.org/wiki/Vibrating_string#Wave

The velocity squared, V^2 = T/rho = tension/mass density

mass density = mass / length

Also, the velocity = wavelength * frequency , so,

velocity/wavelength = frequency

Hope this helps.
 

Thread 'Errors and significant figures'

I multiplied the values first without the error limit. Got 19.38. rounded it off to 2 significant figures since the given data has 2 significant figures. So = 19. For error I used the above formula. It comes out about 1.48. Now my question is. Should I write the answer as 19±1.5 (rounding 1.48 to 2 significant figures) OR should I write it as 19±1. So in short, should the error have same number of significant figures as the mean value or should it have the same number of decimal places as...
View full post »
Thread 'A cylinder connected to a hanging mass'

Thread 'A cylinder connected to a hanging mass'

Let's declare that for the cylinder, mass = M = 10 kg Radius = R = 4 m For the wall and the floor, Friction coeff = ##\mu## = 0.5 For the hanging mass, mass = m = 11 kg First, we divide the force according to their respective plane (x and y thing, correct me if I'm wrong) and according to which, cylinder or the hanging mass, they're working on. Force on the hanging mass $$mg - T = ma$$ Force(Cylinder) on y $$N_f + f_w - Mg = 0$$ Force(Cylinder) on x $$T + f_f - N_w = Ma$$ There's also...
View full post »

Similar threads

Time it Takes for a Transverse Pulse to Travel a Distance "L" Up a Cable Against Gravity?
Replies
13
Views
1K
Waves and vibrations on a string
Replies
2
Views
2K
Standing wave transverse motion and amplitude
Replies
5
Views
2K
Wave function - displacement - transverse wave
Replies
3
Views
2K
Calculating the Total Energy of a Transverse Wave on a String
Replies
6
Views
2K
Finding Tension in a Transverse Wave on a String
Replies
1
Views
2K
How Do You Calculate Max and Min Transverse Speeds in a Wave on a String?
Replies
1
Views
4K
Waves on a String -- Minimizing reflections from the far end (ring on a bar)
Replies
1
Views
2K
How Do You Calculate the Propagation Speed of a Transverse Wave on a String?
Replies
8
Views
2K
Wave equation, wavelenght not given
Replies
6
Views
2K

Hot Threads

Recent Insights

Back
Top