How Do You Calculate the Tension in a Chandelier Cable?

[~angel~]

Hey...I'm having a lot of trouble with a few questions for university physics.

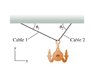
1. A chandelier with mass m is attached to the ceiling of a large concert hall by two cables. Because the ceiling is covered with intricate architectural decorations (not indicated in the figure, which uses a humbler depiction), the workers who hung the chandelier couldn't attach the cables to the ceiling directly above the chandelier. Instead, they attached the cables to the ceiling near the walls. Cable 1 has tension T_1 and makes an angle of theta_1 with the ceiling. Cable 2 has tension T_2 and makes an angle of theta_2 with the ceiling.

Find an expression for T_1, the tension in cable 1, that does not depend on T_2.Express your answer in terms of some or all of the variables m, theta_1, and theta_2, as well as the magnitude of the acceleration due to gravity g.

The image of the chandelier is below.

I would prefer if people could type the working out of the solution as well.

Thank you.

 

[Nylex]

I would prefer if people could type the working out of the solution as well.

People aren't going to do that, you need to show some effort yourself if you want help. You need to resolve forces horizontally and vertically for a start.

 

[ramollari]

~angel~ you didn't demonstrate some initial effort to solve that problem.

In any case I'll give you some guidance:

Write down the equilibrium condition for the horizontal direction (in order to express T2 in terms of T1).
Write down the equilibrium condition for the vertical direction and substitute T2 with the formula in terms of T1. Then solve for T1, and later T2 is easily derived.

 

[~angel~]

I apologise if I appear to have made no effort due to the wording of my question, but I have attempted to work out the answer, even the way you mentioned it ramollari, but I just don't get it.

 

[~angel~]

Sorry if I sounded rude...

 

[Nylex]

Post your working.

 

[~angel~]

tfor the y-coordinates, i got T_2costheta, but this is the same y-coordinate system for T_1costheta. Either way one of those minus M*g, which is directed downwards is equal to 0, because there is no net force. In the x-coordinate system, there is T_1sintheta, and T_2sintheta, and adding those up also results in 0 because there is no net force. From then on, I'm just completely lost. I'm not 100% sure about the coordinate system. That's the part which is confusing me the most.

 

[ramollari]

No, the way the picture is drawn the horizontal components use cos\theta, not the vertical.

OK, let's try it:

Horizontal:

T_1cos\theta _1 = T_2cos\theta _2

T_2 = \frac{cos\theta _1}{cos\theta _2}T1 [1]

Vertical:

T_1sin\theta _1 + T_2sin\theta _2 = mg

T_1 (sin\theta _1 + \frac{cos\theta _1sin\theta _2}{cos\theta _2}) = mg (substitution from [1])

Solve for T_1. Then use [1] to solve for T_2.

 

[~angel~]

No wonder I'm getting all the questions wrong. Thank you so much.

 

[ramollari]

No wonder I'm getting all the questions wrong. Thank you so much.

It was not cos and sin. :-) Your reasoning was wrong (you even included the frictional force into the calculations).

 

[lily_stein]

I'm working on the exact same problem myself, and I've come up with the following:
T_1*sin(theta_1)+T_1*cos(theta_1)*sin(theta_2)/cos(theta_2)-mg

Where did I go wrong? That isn't the right answer, apparently, because I am told that the answer does not depend on the variable T_1, but if it does not depend on T_1 or T_2, what does it depend on?
Thanks
Lily