How Do You Calculate V_D in Terms of Circuit Components and Constants?

[Rawl]

Homework Statement

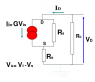
Trying to come up with an equation of V_D in terms R_S, R_d, R_D, V_i, G

G is a constant

Homework Equations

Sum of voltages around a loop = 0
Sum of currents at a node = 0
Voltage divider
Current divider
Resistance of resistors in parallel

The Attempt at a Solution

<br /> V_i = V_D<br />

I'm not exactly sure but if you probe with your voltmeter from the ground to the upper side of V_D and then do the same at the top of the current source. Wouldn't those be the only two components in a loop?

 

[BvU]

Hi Rawl,

Not good you didn't receive an adequate reply yet, so I'll give it a go. The red thingy to me seems to represent a current source, but you forgot to mention that. G is not just a constant, it has a dimension too !

My advice is to redraw the circuit: source at left, the resistors to the right. resistors in series clearly shown in series and parallels visually parallel. Insight will come in a flash !

oh and perhaps upside down to see the relation between V_D and V_is ...

 

[gneill]

Looks like a two node or two loop problem. Either way, two equations in two unknowns with the constraints implied by the $V_{is}$ constraint equation. Since $V_i$ is not specified on the given circuit diagram it presumably is some external value that is part of some other circuit.

Both mesh and nodal methods have their own small advantages here: Nodal analysis would allow you solve for $V_D$ directly and "access" to $V_S$ for applying the constraint, while mesh analysis gives you the current in the small loop as "already solved", since it contains a current source. About the same amount of algebra for each, I'd guess. So pick an analysis method and write some equations.