laura_a
- 64
- 0
Homework Statement
I am a maths teacher retraining in physics, haven't received my textbook yet but attempting the course work, I have the answer to this question and the mathematic skills to solve it, but the notes don't give any worked examples so I have no idea how to go from the law to the answer.
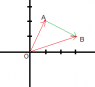
q. A charge q1 is located at x=1 m, y=0. What should you use for the unit vector r in Coulomb's law if you are calculating the force that q1 exerts on charge q2 located at the point x=0 y=1m
Homework Equations
The law I have is F_{12}=[(kq1q2)/r^2]r
The Attempt at a Solution
And I understand the question wants a vector answer and with my maths skills I drew the points and worked out that the distance from q1 to q2 is sqrt(2) and I know the answer is the vector
-sqrt(2)/2 i + sqrt(2)/2 j
Where does the negative come from and why is it over 2? I know this is a silly question but my lecture notes go from the law to this question. I assume the textbook will shed more light but I was just trying to understand this part before moving on.
Thanks to anyone that has time for this :)