Cade Kingston
- 6
- 0
Member advised to use the homework template for posts in the homework sections of PF.
1.
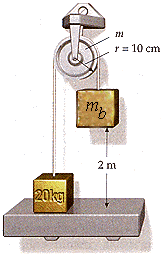
The mb = 25 kg block is 2 m above the ledge. The pulley is a uniform disk with a radius of 10 cm and mass m = 4 kg.
2. (a) Find the speed of the 25 kg block just before it hits the ledge.
(b) Find the angular speed of the pulley at that time.
(c) Find the tensions in the strings.
(d) Find the time it takes for the 25 kg block to reach the ledge. Assume that the string does not slip on the pulley.
3. I know that you are supposed to set up a system of equations with net force and net torque:
20a = T1-20(9.8)
25a = 25(9.8)-T2
.5(4)a=T
The mb = 25 kg block is 2 m above the ledge. The pulley is a uniform disk with a radius of 10 cm and mass m = 4 kg.
2. (a) Find the speed of the 25 kg block just before it hits the ledge.
(b) Find the angular speed of the pulley at that time.
(c) Find the tensions in the strings.
(d) Find the time it takes for the 25 kg block to reach the ledge. Assume that the string does not slip on the pulley.
3. I know that you are supposed to set up a system of equations with net force and net torque:
20a = T1-20(9.8)
25a = 25(9.8)-T2
.5(4)a=T