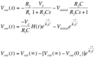- #1
rhysticlight
- 4
- 0
Homework Statement
The problem is shown in the attached PDF, it is basically applying a square wave signal to an op-amp integrator which has a resistor across the capacitor to correct for small DC signal.
In this case it is given that the capacitor has an initial charge of 1 V on it.
Homework Equations
Relevant equations are the transfer function of such an op-amp:
H(S) = [tex]\frac{-R2}{R1}[/tex] [tex]\frac{1}{1+R2_{2}SC}[/tex]
As well as the time domain equation for the output voltage:
Vout = (-1/R1C)*[ integral from 0 to t (Vindt] - Vc
where Vc is the initial voltage across the capacitor
The Attempt at a Solution
So basically I have found three separate ways to solve this problem, but am not sure which one is correct:
First Way
Recognize the fact that the corner frequency of the low pass filter is 0.5 rad/s while the frequency of our input waveform (from 0 to 500 ms) is 4 pi, which is much greater than the corner frequency and we can therefore neglect the shunt resistor and treat this as a simple integrator.
This would leave the same 1 V charge on the capacitor at the end of the waveform, and for 500 ms < t < inifinity, we simply have an exponential decay of this 1 V charge with a time constant of 2 seconds.
Second Way
Draw the circuit in the Laplace domain, which results in us having to add a voltage source in series with the capacitor to account for the initial charge on the capacitor. The expression for the output in the s-domain then becomes:
(see attachment 2)
This reduces to the same expression for my case of 500 ms < t < inifinity, but I don't think it is correct for the other two intervals, but am not quite sure why (I feel like this expression isn't properly accounting for the fact that the capacitor is charging)
Third Way
Use a formula that I got out of the textbook that basically has the form of the final equation in the attached thumbnail. This basically treats the circuit as a simple STC circuit, I feel like the answers I get with this equation should match up with my second method above, but so far they are not.
Clearly I am pretty confused as to how to best approach this problem and would appreciate any advice you can give as everything I have found online or in books doesn't really examine this type of op-amp in this manner (generally just stops after getting the transfer function and noting its characteristics). Sorry for the long and possibly confusing post!
Thanks!