OK, some step by step comments:
wirefree said:
1) Consider diode is always on
OK, that is a reasonable assumption, I guess. We don't know because you never told us the frequency of the AC source. In any case, you can go ahead with your solution with this assumption, but, you MUST verify that the solution you get is compatible with this. Specifically, you will need to look at the diode current and verify that it doesn't ever flow backwards. If that's true then your assumption was correct. If it isn't true then you need to start over without making this assumption.
wirefree said:
You can't forget the DC source. However, because you have assumed that the diode is always on and have replaced it with a battery and/or resistor, then you can solve the circuit with the DC source set to zero and also solve it when the AC source is set to zero. Your final solution will be the sum of these 2 separate solutions. For example, the resistor current will be the current due to the DC source plus the current due to the AC source. This only works if your circuit has the basic (linear) circuit elements (resistors, capacitors, voltage sources, etc.), no diodes, switches, or elements with complex behavior. This analysis technique is called superposition and is probably something you haven't studied yet. It is a powerful principle for all "linear" physics problems (it is actually the definition of "linear" in analysis).
wirefree said:
3) Convert AC, R and C to phasors
OK. Recall that the magnitude of the capacitors phasor (impedance) is a function of the frequency. That's why we asked about that value.
wirefree said:
4) Invert R & C phasor values to obtain admittances. Add them. Invert the result.
Good. That will give you a single impedance value that you can substitute for the R & C parallel combination.
wirefree said:
5) Obtain total current by dividing voltage and impedance phasors from 3 & 4 above
OK. The total current is the current through the diode due to the AC source if the diode is always on. This is half of what you need to verify your initial assumption in step 1. You can compare this t the total current from the DC source to determine if the diode current ever flows backwards.
wirefree said:
6) Invoke current divider for R to obtain current through R
?
Why do you want to know the current through R?
At step 5 you found the total current from the voltage across R||C. Why wouldn't you use the same approach to find the current through R.
Question: If I put 5V across a 2ohm resistor, what is the current through the resistor? If I then add a 1ohm resistor in parallel with the 2ohm resistor, then what is the current through the 2 ohm resistor.
wirefree said:
7) Multiply the last result with R to obtain ripple voltage across R
So you used
the voltage across R in step 5 to find the total current, then you calculated the fraction of that current flowing through R, then you multiplied by R to find
the voltage across R. Think more, calculate less. You are making the problem unnecessarily hard. However, if you did the calculations correctly, you would get the correct voltage.
wirefree said:
8) Divide by sqrt(2) to obtain peak value
This is a typo, right? 1/√2 is about 71%. The peak value is the largest value a quantity can be (in time), which is probably not 71% of something.
OK finally, yes phasors are an important tool. It is important to fully understand the use of phasors (or vectors, or complex numbers, they are all nearly the same thing) in AC circuit analysis. If you continue to study electronics you will have to understand these concepts. They all ultimately come back to working with the magnitude and the phase of sinusoidal waveforms.
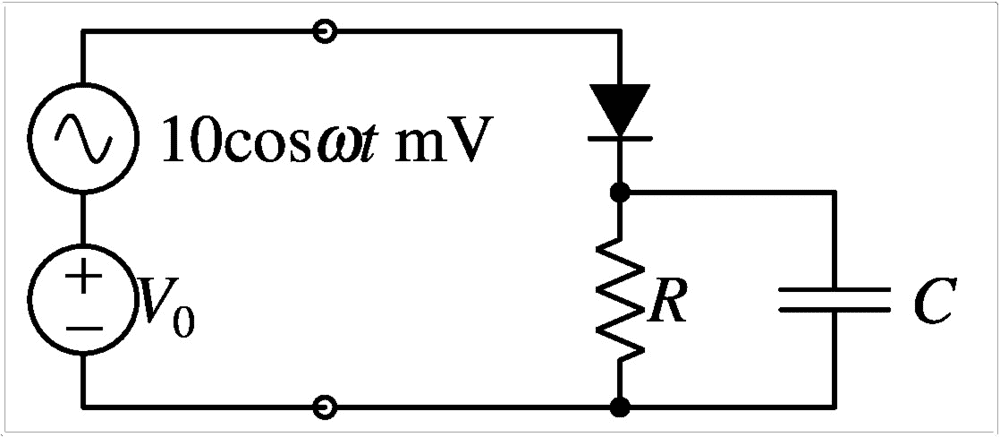 Concepts: Concepts that I am familiar with are related to the diode. The diode circuit I worked on successfully included just a resistor, and so the ripple voltage was found by determining diode current for the DC source and subtracting from it the diode current for the AC source; the result multipled with R gave me the incremental voltage.
Concepts: Concepts that I am familiar with are related to the diode. The diode circuit I worked on successfully included just a resistor, and so the ripple voltage was found by determining diode current for the DC source and subtracting from it the diode current for the AC source; the result multipled with R gave me the incremental voltage.