Peter Dimitrov
- 2
- 0
I have a question about Pascal law. Recenly I was studying and I found this image in my physics book - a copy of the barometer which Torricelli used in his experiment (this is a redraw):
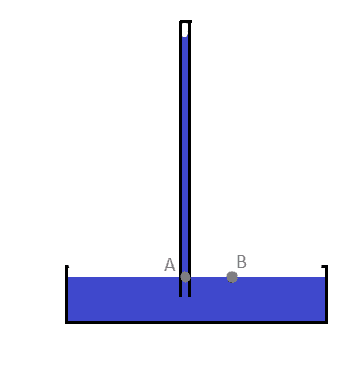
Where the blue thing is the fluid (mercury), while the black thing is the container.
According to my textbook, the pressure at point A is simply (p*g*h), the preasure caused by the fluid above it. However, why don't we also count the atmospheric pressure? Isn't it supossed to act in the entire fluid according to Pascal's law?
Thanks in advance!
Where the blue thing is the fluid (mercury), while the black thing is the container.
According to my textbook, the pressure at point A is simply (p*g*h), the preasure caused by the fluid above it. However, why don't we also count the atmospheric pressure? Isn't it supossed to act in the entire fluid according to Pascal's law?
Thanks in advance!