How Does Catching a Ball Affect the Angular Speed of a Merry-Go-Round?

  • Thread starter Thread starter bewger
  • Start date Start date
AI Thread Summary
The discussion revolves around a physics problem involving a child on a merry-go-round who catches a ball, affecting the system's angular speed. The conservation of angular momentum is emphasized, with the initial angular momentum of the ball needing to be accounted for before and after the catch. The user initially calculates the total rotational inertia but receives feedback indicating a misunderstanding of how to apply angular momentum principles correctly. Clarifications are requested on the distinction between the ball's angular momentum before and after the catch. The conversation highlights the importance of accurately applying conservation laws in rotational dynamics.
bewger
Messages
6
Reaction score
0

Homework Statement


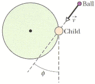
In the figure below, a 30 kg child stands on the edge of a stationary merry-go-round of mass 100 kg and radius 2.0 m. The rotational inertia of the merry-go-round about its rotation axis is 150 kg·m2. The child catches a ball of mass 1.1 kg thrown by a friend. Just before the ball is caught, it has a horizontal velocity v of magnitude 11 m/s, at angle ϕ = 37° with a line tangent to the outer edge of the merry-go-round, as shown. What is the angular speed of the merry-go-round just after the ball is caught?


11-54.gif

Homework Equations


p = mv
L = Iw


The Attempt at a Solution



So I'm assuming that angular momentum is conserved. Thus,

mv = Iw
I found the total I.
I_merrygoaround = 150
I_child = MR^2 = 120
I_ball = MR^2 = 1.1(rsin(phi))^2 = 1.44
I_total = 271.44

\omega = (mv) / (I_total) = 12.1/271.44 = 0.0445 rad/s

But this is incorrect.
What did I do wrong?
 

Attachments

  • 11-54.gif
    11-54.gif
    7.8 KB · Views: 623
Physics news on Phys.org
hi bewger! :smile:

you seem to be mixing up the angular momentum of the ball before with the angular momentum of the ball after :wink:
 
Hi tiny-tim

I'm trying to figure out my mistake with your advice, but I'm a little stumped by what you mean by that.

Can you elaborate on that?
 
hi bewger! :smile:

I'm finding it a little difficult to read what you posted (try using the X2 tag just above the Reply box :wink:), but I don't think you've included both the angular momentum of the ball before and the different angular momentum of the ball after :smile:
 
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Angular momentum conservation on a merry-go-round
Replies
5
Views
2K
Conservation of Angular Momentum -- Child jumping onto a Merry-Go-Round
Replies
18
Views
6K
How Does Angular Momentum Remain Conserved in a Merry-Go-Round System?
Replies
8
Views
2K
Mechanical energy lost when child jumps onto merry-go-round
Replies
3
Views
2K
How Does Moving Towards the Center Affect a Merry-Go-Round's Kinetic Energy?
Replies
1
Views
2K
Magnitude of Acceleration on Merry-Go-Round
Replies
2
Views
2K
Angular momentum changing as mass moves to center
Replies
2
Views
2K
Conservation of Angular Momentum of merry-go-round
Replies
2
Views
3K
Angular momentum merry go round problem
Replies
9
Views
6K
How Does the Coriolis Force Affect a Ball Toss on a Merry-Go-Round?
Replies
18
Views
2K

Hot Threads

Recent Insights

Back
Top