How Does Observer Proximity Affect Clock Synchronization in Different Frames?

[mananvpanchal]

Suppose, a long object is at rest in S frame. There is A (On the long object) and B (Near the long object, on the ground) observer in the middle of the long object. There are two clocks located on both end of long object. We suppose, both A and B is at origin of S frame and clocks at some -x and +x location. The clocks is synchronized for both observer.

Now, at t=0 the object starts moving to right with respect to B observer. Now the long object is at rest in S' frame and moving relative to S frame.

We can see from the diagram that clocks is still synchronized for A observer, but no longer synchronized for B observer. The time reading changed instantly for B. Time decrease in left clock and increase in right clock for B. After the frame change, the difference between the time readings of clocks remains constant for B. We can see that both clocks is far from B in this case.

Now, suppose a situation where observer A, B and left clock are on origin of S. Now A and B is at left end of long object. We can see that left clock reading is not changed instantly for B on frame change, but right clock's reading increases for B. We can see that left clock is near to B in this case.

Now, suppose a situation where observer A, B and right clock are on origin of S. Now A and B is at right end of long object. We can see that right clock reading is not changed instantly for B on frame change, but left clock's reading decreases for B. We can see that right clock is near to B in this case.

In all the case clock reading changed instantly when the clock is not near to the B observer. I think the distance of observer from clocks is the cause of instant change in readings, and direction of motion of clocks is the cause of in which way the clocks desyncs, up or down.

I would like to read your thoughts.

Please, feel free to point out any error if have made here.

 

[Mentz114]

In all the case clock reading changed instantly when the clock is not near to the B observer. I think the distance of observer from clocks is the cause of instant change in readings, and direction of motion of clocks is the cause of in which way the clocks desyncs, up or down.

I'm not sure what point you are making, but instantaneous change in velocity is not possible, requiring an infinite force to be applied for zero time. Clearly not possible.

 

[mananvpanchal]

I'm not sure what point you are making, but instantaneous change in velocity is not possible, requiring an infinite force to be applied for zero time. Clearly not possible.

Yes, instantaneous change in frame is not possible if we describe this with very high speed. If we talk about very low speed then we can describe the diagrams. After all moving condition from steady condition is surely not a smooth transition. We can differentiate the two condition even the speed is very low.

 

[Mentz114]

Yes, instantaneous change in frame is not possible if we describe this with very high speed. If we talk about very low speed then we can describe the diagrams. After all moving condition from steady condition is surely not a smooth transition. We can differentiate the two condition even the speed is very low.

I suppose an infinitesimal change could be thought of as instantaneous, but for observable effects one must integrate these small changes.

I'm sorry but I still don't know what point you are making about the clock synching.

 

[mananvpanchal]

I suppose an infinitesimal change could be thought of as instantaneous, but for observable effects one must integrate these small changes.

Yes, we have to integrate small changes of frames to observe the effect. But, if we talk about small speed (like firing the object from a gun), we can change the frame. Though the effect would not be observable, but still there is theoretical desync would be occurred for B.

I'm sorry but I still don't know what point you are making about the clock synching.

Sorry, I cannot get where is your confusion lies.
If A changes his frame instantly the clocks still would be synchronized for A, but wouldn't be synchronized for B.

BTW Your username suffix is matched with my post counter.

 

[harrylin]

[..]We can see from the diagram that clocks is still synchronized for A observer, but no longer synchronized for B observer. The time reading changed instantly for B. Time decrease in left clock and increase in right clock for B. [..]
In all the case clock reading changed instantly when the clock is not near to the B observer. [..] Please, feel free to point out any error if have made here.

I 'm not sure about what you were saying (sorry), but it sounds as if you misunderstand it, as if you interpret it the wrong way round. No clock reading changes instantly from for example 0:00 to 1:00.

The point is that after acceleration, if one checks the clocks in accordance with the synchronization convention, the clocks will be found to be out of synch according to the definition of this "moving" frame.
Does that help?

 

[Mentz114]

BTW Your username suffix is matched with my post counter.

Not for long, I suspect

Regarding the synchronisation, I'm not surprised that spatial separation plays a part in desynching.

 

[darkhorror]

Are you just wanting to know if your thinking is correct, and that the clocks won't be in sync if frames of reference are changed?

 

[pervect]

Suppose, a long object is at rest in S frame. There is A (On the long object) and B (Near the long object, on the ground) observer in the middle of the long object. There are two clocks located on both end of long object. We suppose, both A and B is at origin of S frame and clocks at some -x and +x location. The clocks is synchronized for both observer.

I have the feeling (perhaps I'm incorrect), that you are envisioning the clock A, and the (unnamed?) clock, which I will call clock "X", that's at the other end of "the long object" from A as being two clocks on a single long and rigid object.

You didn't specify that the object was 'rigid', so perhaps I'm misinterpreting you.

Of course, there is no such thing as a rigid object in special relativity. If you push on one end of a steel rod, the other end will start to move only after a time delay, the time being based on the speed of sound in the steel. You can look it up - it's a lot slower than the speed of light.

I find it less confusing to avoid mentioning extended objects at all, and to talk about two rocketships, A, and X. Both of them are initially at rest, sharing a frame together, and both of them start accelerating really hard when they receive a light signal emitted from their midpoint (the midpoint in their shared initial frame). They accelerate so hard that they burn through their fuel in a very small amount of proper time - and they have a certain delta-v capability, so when they both stop accelerating, they have the same velocity,.

Taking this line of approach, you'll see that the proper distance between A and X changes in this scenario - it's a variant of what's commonly called the "Bell Spaceship Paradox".

Other than possible confusions arising about the notion of "objects", which may or may not be being presumed to be rigid, I don't see anything wrong that I noticed with the space-time diagrams.

If you think of A and X as separate rocketships, it's correct to note that they start accelerating at the "same time" only in the initial frame, and that in the final frame (the frame shared by both after both rocketships have burned all their fuel), they did NOT start accelerating at the same time.

 

[yuiop]

Suppose, a long object is at rest in S frame. There is A (On the long object) and B (Near the long object, on the ground) observer in the middle of the long object. There are two clocks located on both end of long object. We suppose, both A and B is at origin of S frame and clocks at some -x and +x location. The clocks is synchronized for both observer.

Now, at t=0 the object starts moving to right with respect to B observer. Now the long object is at rest in S' frame and moving relative to S frame.

View attachment 45518

We can see from the diagram that clocks is still synchronized for A observer, but no longer synchronized for B observer.

The bold part is not correct. When A and the long rod accelerates the clocks at rest with the rod do not remain synchronised from the point of view of A (or B), if the rod maintains its proper length. The diagrams you have drawn are for the situation where A and B have had constant relative motion forever (no acceleration) and have synchronised their respective clocks in their own rest frames. Each time a system accelerates to a new relative velocity, the clocks have to be resynchronised. Clocks do not automatically jump into the future at the front and into the past at the rear. When a system accelerates while maintain proper length (Born rigid motion) the clocks at the rear naturally advance more slowly than the clocks at the front, because length contraction requires the clocks at the back to accelerate more rapidly than those at the front. No clocks go backwards in time even though a naive interpretation of spacetime diagrams might give that impression.

The time reading changed instantly for B. Time decrease in left clock and increase in right clock for B. After the frame change, the difference between the time readings of clocks remains constant for B. We can see that both clocks is far from B in this case.

View attachment 45519

Now, suppose a situation where observer A, B and left clock are on origin of S. Now A and B is at left end of long object. We can see that left clock reading is not changed instantly for B on frame change, but right clock's reading increases for B. We can see that left clock is near to B in this case.

You need to take care when talking talking about what B (or any observer) sees about events that are not local. Far away events are subject to light travel times and the times of those events require synchronised clocks that are not present in an accelerating system, because they go out of sync during the acceleration and require finite time to resynchronise the clocks and this resynchronisation time is longer than the time intervals under consideration in an accelerating system which is effectively a moving target. It is better to talk about times in a given reference frame which is effectively a matrix of observers that are individually local to all events rather than talk about the observations of a single observer in isolation. Most formulas in relativity such as the Lorentz transformations assume this matrix of an infinite number of local synchronised clocks and so do not involve light travel times.

View attachment 45520

Now, suppose a situation where observer A, B and right clock are on origin of S. Now A and B is at right end of long object. We can see that right clock reading is not changed instantly for B on frame change, but left clock's reading decreases for B. We can see that right clock is near to B in this case.

In all the case clock reading changed instantly when the clock is not near to the B observer. I think the distance of observer from clocks is the cause of instant change in readings, and direction of motion of clocks is the cause of in which way the clocks desyncs, up or down.

As above they do not desync down if by "down" you mean backwards in time. Some clocks advance at a slower rate than others during acceleration but never backwards in time. They only go backwards when somebody resynchronises the clocks manually and winds the clock hands backwards. There is nothing magical going on here.

 

[mananvpanchal]

I 'm not sure about what you were saying (sorry), but it sounds as if you misunderstand it, as if you interpret it the wrong way round. No clock reading changes instantly from for example 0:00 to 1:00.

There may be two possibilities the diagrams is wrong or I have interpreted it wrong way. Please, tell me what might be the problem with my interpretation.

The point is that after acceleration, if one checks the clocks in accordance with the synchronization convention, the clocks will be found to be out of synch according to the definition of this "moving" frame.
Does that help?

Which one? A or B? A is on long object and B is on ground near the object. Now B changes its frame. So what does A see? And what does B see?

 

[mananvpanchal]

Not for long, I suspect

Regarding the synchronisation, I'm not surprised that spatial separation plays a part in desynching.

Yes, desync is not a surprise. But I am surprised with left clock's decreased reading and right clock's increased reading.

 

[mananvpanchal]

Are you just wanting to know if your thinking is correct, and that the clocks won't be in sync if frames of reference are changed?

Yes.

 

[harrylin]

There may be two possibilities the diagrams is wrong or I have interpreted it wrong way. Please, tell me what might be the problem with my interpretation.

See also the elaboration by yuiop. I did not carefully look at your diagrams, and I told you what might be the problem but I'll elaborate.

Which one? A or B?

The point is that after acceleration, if one checks the clocks in accordance with the synchronization convention, the clocks will be found to be out of synch according to the definition of A's new rest frame (due to the object's length contraction also very slightly out of synch according to B's rest frame, but that's not the issue here).

A is on long object and B is on ground near the object. Now B changes its frame. So what does A see? And what does B see?

Likely each only sees a blur. However, they use measurements to draw conclusions. A will simply see and measure that B is moving, as B is not on a long object; so I don't know what you mean with that. And B will measure that the clocks of A are out of synch, if B adapts its measurements to that of a "moving" frame. Except if the motion is perpendicular, for then A's clock times will be measured as equally shifted.

Of course you could ask an infinite number of variant questions like that, so it's not useful to ask more - you will be able to reply them all once you understand these two.

 

[Dale]

I'm not sure what point you are making, but instantaneous change in velocity is not possible, requiring an infinite force to be applied for zero time. Clearly not possible.

Hi Mentz114, just looking at this thread. Although you are correct that it isn't possible, it is a reasonable approximation. Suppose we were talking about a journey of several light years and an acceleration to .6 c in a matter of a few minutes. The approximation would be reasonable as long as we just keep in the back of our head that it is an approximation and we don't look too carefully at those few minutes of acceleration.

 

[Dale]

If A changes his frame instantly the clocks still would be synchronized for A, but wouldn't be synchronized for B.

This is not true, in general. It depends on the details of the acceleration of the clocks and A. In fact, under the acceleration profile as described in the OP the opposite is true.

Btw, there is never a gap in a worldline, and clock readings never change instantaneously in any frame. Your diagrams are wrong.

 

[mananvpanchal]

I have the feeling (perhaps I'm incorrect), that you are envisioning the clock A, and the (unnamed?) clock, which I will call clock "X", that's at the other end of "the long object" from A as being two clocks on a single long and rigid object.

Actually, here the A and B is observer's name.

I find it less confusing to avoid mentioning extended objects at all, and to talk about two rocketships, A, and X. Both of them are initially at rest, sharing a frame together, and both of them start accelerating really hard when they receive a light signal emitted from their midpoint (the midpoint in their shared initial frame). They accelerate so hard that they burn through their fuel in a very small amount of proper time - and they have a certain delta-v capability, so when they both stop accelerating, they have the same velocity,.

Taking this line of approach, you'll see that the proper distance between A and X changes in this scenario - it's a variant of what's commonly called the "Bell Spaceship Paradox".

Other than possible confusions arising about the notion of "objects", which may or may not be being presumed to be rigid, I don't see anything wrong that I noticed with the space-time diagrams.

If you think of A and X as separate rocketships, it's correct to note that they start accelerating at the "same time" only in the initial frame, and that in the final frame (the frame shared by both after both rocketships have burned all their fuel), they did NOT start accelerating at the same time.

Yes, we can generate the scenario of three rockets. There are three rockets left, middle and right. Left and right rocket has one one clock. A observer in middle rocket. And B observer on ground near middle rocket. Now both clocks is synchronized for both observers. Now rocket starts moving (ignore gravitation force) with constant speed (I know high speed from rest state is not possible, so we can guess it as less speed). Now all three rockets in S' frame. The diagram shows that both clock is still synchronized for A, but not for B.

Actully, here I don't want very high speed, and I don't want to accelerate for much time. I need here less speed with instant change.

 

[mananvpanchal]

The diagrams you have drawn are for the situation where A and B have had constant relative motion forever (no acceleration) and have synchronised their respective clocks in their own rest frames.

Yes, if we see diagram after t=0, it will look like B has came from far with his synchronized clocks. I have combined two diagram, in one A is at rest in S frame and in second A is moving relative to S frame.

When A and the long rod accelerates the clocks at rest with the rod do not remain synchronised from the point of view of A (or B), if the rod maintains its proper length

Each time a system accelerates to a new relative velocity, the clocks have to be resynchronised. Clocks do not automatically jump into the future at the front and into the past at the rear. When a system accelerates while maintain proper length (Born rigid motion) the clocks at the rear naturally advance more slowly than the clocks at the front, because length contraction requires the clocks at the back to accelerate more rapidly than those at the front. No clocks go backwards in time even though a naive interpretation of spacetime diagrams might give that impression.

So, can you explain me in which pattern the clocks become desync for A and B (with scenario of constant acceleration and with scenario of instant frame change)?

There is nothing magical going on here.

That is why I need your thoughts.

 

[Dale]

mananvpanchal, I already explicitly derived the synchronization for this exact scenario for you (assuming an instantaneous acceleration from 0 to .6c) here starting with post 42:
https://www.physicsforums.com/showthread.php?t=581451&page=3

You responded several times and I clarified each of your quesitons, so you already were aware that your statements in the OP are incorrect. I don't know why you made them.

 

[mananvpanchal]

This is not true, in general. It depends on the details of the acceleration of the clocks and A. In fact, under the acceleration profile as described in the OP the opposite is true.

Can you elaborate more?

Btw, there is never a gap in a worldline, and clock readings never change instantaneously in any frame. Your diagrams are wrong.

Are you talking about gap between right clock's world line in S and S'?

 

[mananvpanchal]

mananvpanchal, I already explicitly derived the synchronization for this exact scenario for you (assuming an instantaneous acceleration from 0 to .6c) here starting with post 42:
https://www.physicsforums.com/showthread.php?t=581451&page=3

You responded several times and I clarified each of your quesitons, so you already were aware that your statements in the OP are incorrect. I don't know why you made them.

Because, I think there was very big misunderstanding happened. And finally we couldn't reach to the answer.

 

[darkhorror]

Why not have clocks on the ground frame, and on the spaceships. Then have the spaceships moving at constant velocity with respect to the ground. Start by looking at it from the ground frame then switch to looking at it from the spaceships. That way you wouldn't have to deal with acceleration. Plus it may make what you are wondering easier to see since you have clocks on both.

 

[Dale]

Because, I think there was very big misunderstanding happened. And finally we couldn't reach to the answer.

Really, I thought we ended the thread in complete agreement. Since the thread wasn't locked I am surprised to see this thread, both that there is still disagreement and that you didn't ask more questions there.

So what are your remaining questions? Did you still not follow the math?

 

[Dale]

Are you talking about gap between right clock's world line in S and S'?

Yes. For the clock on the left, a few moments before t=0 suddenly a second copy appears, and there are two left clocks until t=0 when the original one suddenly disappears. Meanwhile, at t=0 the clock on the right disappears, and there is nothing there until suddenly a few moments later it reappears.

Obviously that is all very non-physical. Worldlines are continuous, they don't jump or have gaps, not even in non-inertial frames.

 

[mananvpanchal]

Yes. For the clock on the left, a few moments before t=0 suddenly a second copy appears, and there are two left clocks until t=0 when the original one suddenly disappears. Meanwhile, at t=0 the clock on the right disappears, and there is nothing there until suddenly a few moments later it reappears.

Obviously that is all very non-physical. Worldlines are continuous, they don't jump or have gaps, not even in non-inertial frames.

If I agree with this, and you have said that

This is not true, in general. It depends on the details of the acceleration of the clocks and A. In fact, under the acceleration profile as described in the OP the opposite is true.

Now I need to understand how can I describe Minkowsky diagram from your conclusion?

 

[mananvpanchal]

Why not have clocks on the ground frame, and on the spaceships. Then have the spaceships moving at constant velocity with respect to the ground. Start by looking at it from the ground frame then switch to looking at it from the spaceships. That way you wouldn't have to deal with acceleration. Plus it may make what you are wondering easier to see since you have clocks on both.

From this post I get an idea of easy description to evaluate the problem.

Suppose, Now A, B, left clock and right clock are at rest in S frame. A and B at origin and left clock is at some -x and right clock is at some +x. Now at t=0 B changes his frame from S to S'. Now B sees left clocks reading as as t'L and sees right clock reading as t'R. Now here is no accelerating clocks involved and no gap between world lines involved. Now, this is just the issue of Lorentz transformation.

Uptill now I get different opinions about desync from you guys.

Regarding the synchronisation, I'm not surprised that spatial separation plays a part in desynching.

I don't see anything wrong that I noticed with the space-time diagrams.

When A and the long rod accelerates the clocks at rest with the rod do not remain synchronised from the point of view of A (or B), if the rod maintains its proper length.

I did not carefully look at your diagrams, and I told you what might be the problem but I'll elaborate.

This is not true, in general. It depends on the details of the acceleration of the clocks and A. In fact, under the acceleration profile as described in the OP the opposite is true.

And I am really confused now. Now we have to come to one resolution, there should not be different outcome per person.

 

[harrylin]

[..] Uptill now I get different opinions about desync from you guys.

And I am really confused now. Now we have to come to one resolution, there should not be different outcome per person.

No, your summary doesn't match well what we said (if anything) about the desync; for example you cited a completely different part than what I explained twice to you about desync.
Instead of different opinions, no-one here disagreed with the opinion of at least three of us that your phrase "We can see from the diagram that clocks is still synchronized for A observer", is wrong:

- The diagram doesn't tell us about effects of acceleration (at least not directly).
- The effect is that the clocks clocks are not anymore synchronized for the A observer if he verifies them with the standard synchronization for the new rest frame.
- What we can see from the diagrams: the standard synchronization of the new rest frame (in which A is now in rest) differs from that of the old rest frame (in which A is now in rest).

 

[Dale]

If I agree with this, and you have said that


Now I need to understand how can I describe Minkowsky diagram from your conclusion?

The best way is to plot the worldlines and label the clock readings that I derived in the other thread.

 

[yuiop]

Uptill now I get different opinions about desync from you guys.
...

And I am really confused now. Now we have to come to one resolution, there should not be different outcome per person.

Mananvpanchal, there are number of things you have to specify to clear up the confusion, otherwise people are having to guess what you are asking and hence the different answers.

First you have to specify the acceleration method of which there are two basic types (and anything in between).

Type 1 acceleration:
This requires that the rod maintains its proper length at all times. This is officially known as "Born Rigid acceleration" in the literature and you can google it. An inertial (un-accelerated) observer (at rest in frame S) will see the clock at the back of the rod tick slower than the clock at the front of the rod. An observer riding on the accelerating rod (momentarily at rest in frame S') will also see clocks at the front tick faster than clocks at the back. Neither type of observer sees the clocks as remaining in synchronisation because it is impossible for clocks that tick at different rates to remain in sync. This is essentially equivalent to being in a gravitational field with clocks higher up ticking faster than clocks lower down. This form of acceleration does not match the conclusions you draw in your original post.

Type 2 acceleration:
In this acceleration method the rod maintains its measured length in frame S as measured by an inertial (un-accelerated) observer at rest in that reference frame. This form of acceleration is not sustainable as the rod will eventually be torn apart (even though it appears to keep constant length). This is essentially the situation in Bell's spaceship paradox as mentioned by Dalespam. In this form of acceleration, the accelerating clocks remain in sync from the the point of view of the un-accelerated observer at rest in ref frame S and they are not in sync from the point of view of the observer at rest with the accelerating rod. This follows from the fact that if two clocks are synchronised in one reference frame they cannot be synchronised in another reference frame that has relative motion. This form of acceleration is also not compatible with your conclusion in your opening post and is in fact the exact opposite.

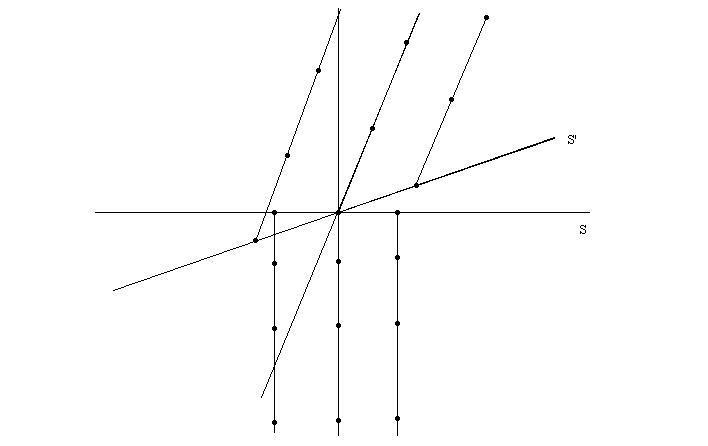
In your opening post you said "We can see from the diagram that clocks is still synchronized for A observer" where A is the observer on the accelerating rod and from the above you can see that neither basic acceleration method can keep the clocks synchronised from A's point of view. As you have not specified an acceleration method it seems clear that you are not even aware that there are different acceleration methods that yield different results.

Later you state "I think the distance of observer from clocks is the cause of instant change in readings, and direction of motion of clocks is the cause of in which way the clocks desyncs, up or down." This makes me think you are under the impression that clocks can go backwards. Just to clarify, there are no circumstances under which an observer sees a clock go backwards, they can only slow down.

Next you have to clarify if by "see" you mean what a single observer literally sees which requires light travel times to be taken into account and to analyse those sort of observations is more difficult than the standard Lorentz transforms which do not include light travel times. Is that you intention? If that is what you mean then there are some things you have to consider which I will illustrate by way of example. Let us say that the rod is one light second long and A is at the back of the rod. Clocks at the front and back of the rod are synchronised. Before the rod accelerates, A sees the clock at the front read one second behind the clock at the back that he standing next to. Now if the rod accelerates very rapidly for a short period of time, he will feel and see the back of the rod accelerating and the front of the rod will still be stationary (because he is seeing the front of the rod, one second in the past, even when it is stationary). The clock next to him at the back slows down when the rod starts to accelerate, but he is not aware of this because it is his local time. Now because he seeing the clock at the front one second in the past, he is seeing light signals from that clock before it started accelerating so it was still ticking normally but because he going towards it and because his own local/internal clocks have slowed down it will look like the clocks at the front have started ticking faster than normal. Hopefully you can now understand the complications that come about if you insist on asking what a single observer "sees" rather than what a set of co-moving observers measure.

You also seem to quite frequently talk about an observer "instantly switching" reference frames which is very vague and meaningless unless you specify how that that observer "switches" frames, which means you have to specify the acceleration method and then follow that up with how the measurements are made.

As I mentioned before, when an extended object accelerates, the clocks become desychronised. The diagrams you are using are for reference frames with synchronised clocks in steady state motion. You cannot switch instantly from one reference frame to another, even with extreme power and expect it to look anything like your diagrams and I will explain with another example. Let us retain the one light second long rod. Let us say it accelerates to 0.6c in one nanosecond. (Difficult but not impossible in principle). The clocks would instantly go out of sync and to re-synchronise the clocks at the back and the front would require sending a light signal from the back to the front to establish the round trip time for the signal and another signal from the back to the front for the sychronisation signal. The whole process of re-sychronisation would take in the order of 3 seconds so it is impossible to switch frames in one nanosecond and expect the clocks to be re-sychronised in that time. You could skip the initial two way signal and just assume the length is unchanged but even then the re-sychronisation process would take about a second which not exactly the "instantaneous" switch you are looking for.

Hopefully you are now aware why transforming from the point of view of one observer to the point point of view of a different observer in constant relative motion Minkowski charts of two systems in constant relative motion and assuming that is what it would look like is nothing like what you get if you literally get a single observer to "instantly" and literally switch reference frames. It just does not work.

It would also help if you would clarify that you understand that a Minkowski chart is NOT the point of view an individual observer, or what any given observer "sees" at any given time, but is rather the pooled results of a multitude of co-moving observers that are individually local to the events under consideration and who compare notes on times of events long after those events took place.

It seems there are many factors you are not aware and I am sure this is the source of the confusion in this thread.

P.S. Why have we all got the same girly avatar? :O

 

[harrylin]

[..]- What we can see from the diagrams: the standard synchronization of the new rest frame (in which A is now in rest) differs from that of the old rest frame (in which A is now in rest).

Oops sorry for the glitch! Corrected:
- What we can see from the diagrams: the standard synchronization of the new rest frame (in which A is now in rest) differs from that of the old rest frame (in which A is now moving)