idlackage
- 10
- 0
Launching a projectile while on something with velocity
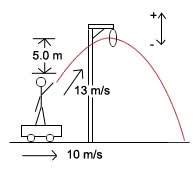
A man is riding on a cart which is moving at a constant velocity of 10 m/s. He wishes to throw a ball through a stationary hoop 5.0 m above his extended hand in such a manner that the ball will be at the top of its trajectory as it passes through the hoop. He throws the ball with a speed of 13 m/s with respect to himself.
a) What must be the vertical component of the initial velocity of the ball?
b) How many seconds after he releases the ball will it pass through the hoop?
c) At what horizontal distance in front of the hoop must he release the ball?
V1 = V2 - a⌂t
⌂d = V1⌂t + 0.5a⌂t2
I pretty much have nothing but that diagram. I have no idea how to even start--I attempted making sense of a triangle calculation somewhere with the givens, but it didn't work out.
Parts b) and c) would be done using one of the 'relevant equations' since I'm guessing I'd obtain the necessary information to plug into them after doing part a).
Thanks for any help.
Homework Statement
A man is riding on a cart which is moving at a constant velocity of 10 m/s. He wishes to throw a ball through a stationary hoop 5.0 m above his extended hand in such a manner that the ball will be at the top of its trajectory as it passes through the hoop. He throws the ball with a speed of 13 m/s with respect to himself.
a) What must be the vertical component of the initial velocity of the ball?
b) How many seconds after he releases the ball will it pass through the hoop?
c) At what horizontal distance in front of the hoop must he release the ball?
Homework Equations
V1 = V2 - a⌂t
⌂d = V1⌂t + 0.5a⌂t2
The Attempt at a Solution
I pretty much have nothing but that diagram. I have no idea how to even start--I attempted making sense of a triangle calculation somewhere with the givens, but it didn't work out.
Parts b) and c) would be done using one of the 'relevant equations' since I'm guessing I'd obtain the necessary information to plug into them after doing part a).
Thanks for any help.
Last edited: