How Does Retracting Robot Arms Affect Angular and Linear Momentum?

[Joymaker]

Here's a little thought experiment that highlights a problem I'm having with angular momentum.

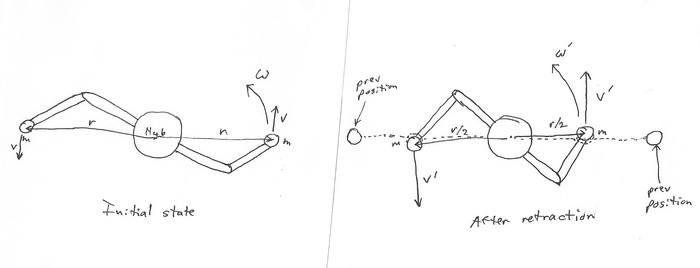
Here's my little experimental gizmo, spinning freely and leisurely in space. It has a hub and a pair of robot arms (whose mass we can ignore) holding a pair of masses m each at a distance r from the center. It is spinning with angular velocity ω, so that each mass is moving with speed v = rω. We'll view it at a snapshot in time when the radius vector lies along the X axis.

At a command from me, my gizmo will retract the robot arms until each mass is now r/2 from the center. It can do it very fast, so fast that only a tiny fraction of one rotation will have taken place during that time. 1°, let's say, just for example.

Now here's the problem. Regardless of the kinetic energy that was generated and wasted retracting the arm so fast, all that took place in the X direction (approximately). But my mass was moving with a linear momentum of p = mv in the Y direction. So this should be unchanged. We should now have r' = r/2, v' = v, ω' = v'/r' = 2ω. Spinning twice as fast as it used to be, which seems perfectly logical.

But no! Conservation of angular momentum works with the quantity Moment of Inertia: I = mr². It declares that L = Iω = mvr is conserved. So once I have pulled in my masses, r' = r/2, v' = 2v, ω' = v'/r' = 4ω. My gizmo is now spinning four times as fast as it used to be. And the momentum of my mass in the Y direction is now p' = mv' = 2mv. How is it possible? How did a radial force (robot arm, pulling along X) give rise to a tangential acceleration (mass, moving faster along Y)? Seems to violate the laws of linear momentum!

 

[VantagePoint72]

You are only considering half the system. You have two masses moving in opposite directions, for a total linear momentum of zero at every moment. The total momentum is still zero after the system contracts and so linear momentum is conserved. There is no reason to expect the linear momentum of either of the masses by themselves to be conserved because they are not isolated from one another.

 

[VantagePoint72]

As for your other question—where does the tangential force come from that changes the tangential velocity of one of the masses—well, you sort of answered that yourself: "It can do it very fast, so fast that only a tiny fraction of one rotation will have taken place during that time." A tiny fraction is not instantaneous, and instantaneous motion of the mass is not possible. It is true that you can, in theory, contract your gadget faster and faster so that the tangential direction changes very little during the contraction; however, to do that your gadget's arms must apply a greater force to the mass during that shorter time period. If the gadget is fully contracted after rotating through 1 degree, then it is true that the component of the contracting force at earlier times parallel to the tangential velocity at later times is very small. However, the total force must be very large to contract it that quickly, so this parallel component—though relatively small—is not negligible.

 

[jartsa]

Let's consider the right arm.

It's oriented as in the picture, when the pulling starts.

The pull gives the mass a velocity to the left.

Next the the arm stops the motion of the mass towards the center by pushing. (note: towards the center, not left)

The push gives the mass a small velocity upwards, and cancels almost all of the velocity to the left that was caused by the pull.

So after the pull and the push the mass has a small additional velocity to the left and a small additional velocity upwards.