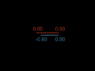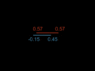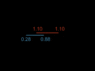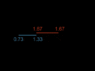I How Does Special Relativity Challenge Our Understanding of Absolute Time?

[name123]

As I understand it with an orthodox interpretation of Special Relativity, if in flat space there was a velocity difference between two inertial frames of reference, then observers in either could calculate the clocks in the other to be going slower. And it could be said that both views are correct, as the truth of the matter would be relative.

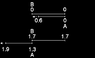
The problem I am having is understanding how such an interpretation could be considered true in the following scenario. Consider 4 spaceships named ShortnegX, LongnegX, ShortposX and LongposX. They are all together and synchronise their clocks with one another and then at t=1 depart. ShortnegX and LongnegX quickly accelerating to a velocity of -v in the -x direction, which ShortposX and LongposX also undergo the same acceleration only in the +x direction and they accelerate to a velocity of +v. At a distance of 1/2x ShortnegX and ShortPosX both decelerate and the accelerate again in the opposite direction heading back to the start position at a velocity of +v and -v respectively. LongnegX and LongposX continue until a distance of x from the starting point has been reached before they quickly decelerate and then accelerate in the opposite direction and head back to the starting point in the same way as ShortnegX and ShortposX had done.

The problem I have with the idea of relative truth here is that as I understand it the relative truth for ShortnegX for example would be that where the ships had been moving at a constant velocity the clock (both on the outward journey and on the inward journey) on ShortposX had been "ticking" slower than its own, and so should be indicating less time had passed than its own when they meet up. But its apparent relative truth would be shown to be wrong when they meet up. The same with ShortposX's relative truth regarding the clocks of ShortnegX. The same with LongnegX regarding the ticking of the LongposX's clock, though here the time difference would be expected to be even bigger than that expected by ShortnegX. Yet it too would be shown to be wrong when they met up. I find it hard to imagine that the accelerations and decelerations could explain it, as they would be the same for both LongnegX and ShortnegX and also the same for LongposX and ShortposX, and yet the differences in time that would needed to be adjusted for LongnegX's relative truth, and ShortnegX's relative truth would be different.

I was wondering if anyone here could explain to me where I have gone wrong in my assessment if indeed I have.

 

[Dale]

I don’t recognize “relative truth” as a standard term in SR. Do you mean “reference frame”?

Your scenario is simply a bunch of twin paradoxes in parallel. The resolution is exactly the same:

http://math.ucr.edu/home/baez/physics/Relativity/SR/TwinParadox/twin_paradox.html

 

[Ibix]

You missed the relativity of simultaneity. If you switch inertial reference frames, as you are doing, your idea of "the same time as I turn round" changes. If you don't remember that fact, you have forgotten to account for a chunk of time on everyone else's worldline.

As Dale notes, this is just a bunch of twin paradox scenarios running at the same time. Apart from the book-keeping it's no more complicated. I recommend learning to draw Minkowski diagrams. That was the tool that finally showed me how simple all this stuff really is, even if it looks ridiculously complex at first glance.

Edit: I wrote a bit of javascript to draw Minkowski diagrams years ago. If you scroll down to "the triplet paradox" there's a button to click to set up half of your scenario - a stay at home and two ships in opposite directions. Select an outbound line and click the "Boost to selected line rest frame". Then select the inbound line and boost again. Note that in the first case, "at the same time as the turnaround" the other ship hasn't turned around yet. In the latter case, "at the same time as the turnaround" the other ship turned around some time ago. This is the point I made above.

Edit 2: link might be useful: http://ibises.org.uk/Minkowski.html

 

[name123]

You missed the relativity of simultaneity. If you switch inertial reference frames, as you are doing, your idea of "the same time as I turn round" changes. If you don't remember that fact, you have forgotten to account for a chunk of time on everyone else's worldline.

As Dale notes, this is just a bunch of twin paradox scenarios running at the same time. Apart from the book-keeping it's no more complicated. I recommend learning to draw Minkowski diagrams. That was the tool that finally showed me how simple all this stuff really is, even if it looks ridiculously complex at first glance.

Edit: I wrote a bit of javascript to draw Minkowski diagrams years ago. If you scroll down to "the triplet paradox" there's a button to click to set up half of your scenario - a stay at home and two ships in opposite directions. Select an outbound line and click the "Boost to selected line rest frame". Then select the inbound line and boost again. Note that in the first case, "at the same time as the turnaround" the other ship hasn't turned around yet. In the latter case, "at the same time as the turnaround" the other ship turned around some time ago. This is the point I made above.

I understand that frames of reference have been changed, and thus what would be regarded as simultaneous has. For clarity on where they turn around the points they turn around can be considered to be simultaneous in the original frame of reference.

What I think I had failed to appreciate was that the observer on ShortnegX would agree that the spacetime interval for its outward journey was the same as the spacetime interval for its inward journey. And both of those were the same as the spacetime interval for ShortposX's outward journey and inward journey. I assume that with Special Relativity a time difference would only appear on clocks if synched at event 1 and then compared at event 2 the spacetime interval for each of their journeys was different. Since the spacetime intervals of their journeys would be the same, the same amount of time would be expected to have passed on their clocks.

As a side note, could that not be used as a definition of simultaneity? In the sense that if two clocks were synched at event 1 then events at the same spacetime intervals from event 1 will also be in synch? Or does that not work?

Edit: Ok, I guess that would not work, as events at the same spacetime intervals from event 1 could be arrived at by journeys of different spacetime intervals. Would perhaps clocks which have traveled the same spacetime intervals be in synch?

 

[SlowThinker]

As a side note, could that not be used as a definition of simultaneity? In the sense that if two clocks were synched at event 1 then events at the same spacetime intervals from event 1 will also be in synch? Or does that not work?

Edit: Ok, I guess that would not work, as events at the same spacetime intervals from event 1 could be arrived at by journeys of different spacetime intervals. Would perhaps clocks which have traveled the same spacetime intervals be in synch?

It's not hard to define simultaneity using light pulses and clocks. What you can't do is define absolute simultaneity. For all we know, all 4 ships could have been moving at 0.9c relative to me before the experiment started.

A clock moving from event 1 to event 2 at a steady pace will show more time than clock that waited until last possible moment, and then accelerated to near light speed to arrive exactly at event 2. Same if it goes to place of event 2 first and then waits for the right time.

 

[PeterDonis]

Would perhaps clocks which have traveled the same spacetime intervals be in synch?

Only if they are at rest relative to each other.

 

[Ibix]

What I think I had failed to appreciate was that the observer on ShortnegX would agree that the spacetime interval for its outward journey was the same as the spacetime interval for its inward journey. And both of those were the same as the spacetime interval for ShortposX's outward journey and inward journey.

Everybody would agree on this. That's the meaning of "invariant".

I assume that with Special Relativity a time difference would only appear on clocks if synched at event 1 and then compared at event 2 the spacetime interval for each of their journeys was different. Since the spacetime intervals of their journeys would be the same, the same amount of time would be expected to have passed on their clocks.

Yes. I'm a bit confused why this gave you difficulty with your original scenario, but fine.

As a side note, could that not be used as a definition of simultaneity? In the sense that if two clocks were synched at event 1 then events at the same spacetime intervals from event 1 will also be in synch? Or does that not work?

You could use that as the basis of a coordinate system, although I think you'd need to be very careful about the details of how you specified it. And it could only cover the future and past light cones of event 1, not all of spacetime. And it wouldn't in general, correspond to any intuitive notion of simultaneity, and would be different from Einstein's notion of simultaneity.

Edit: Ok, I guess that would not work, as events at the same spacetime intervals from event 1 could be arrived at by journeys of different spacetime intervals. Would perhaps clocks which have traveled the same spacetime intervals be in synch?

If the clocks meet up again then yes, their readings will be the same (although tick rates at meet up will differ in general, as Peter notes).

But you don't need a definition of simultaneous for an event. It's when the clocks aren't currently at the same location that you need a definition of simultaneity. As I said, you could use the plane equidistant (equi-interval?) from event 1 as a plane of equal time coordinate, but I don't think it would be an inertial coordinate system, and it would be mathematically more complex for no particular gain.

 

[name123]

It's not hard to define simultaneity using light pulses and clocks. What you can't do is define absolute simultaneity. For all we know, all 4 ships could have been moving at 0.9c relative to me before the experiment started.

A clock moving from event 1 to event 2 at a steady pace will show more time than clock that waited until last possible moment, and then accelerated to near light speed to arrive exactly at event 2. Same if it goes to place of event 2 first and then waits for the right time.

Ok thanks.

But I am still slightly confused because what if the ShortnegX etc., example were imagined in a slightly different way. With a spaceship called Synch which can be considered to be at rest at event 1 with ShortnegX and ShortposX passing each other. ShortnegX traveling in the -x direction at velocity -v and ShortposX traveling in the +x direction at velocity v (from Synch's perspective/frame of reference).

It could also be considered from ShortnegX's frame of reference, where ShortposX passes it at 2v and Synch at v. ShortposX would then be considered to decelerate to rest and ShortnegX to accelerate to 2v. They would all be at synch at event2 even though ShortnegX was at rest for the time it took Synch to travel half the spacetime interval between event1 and event2 but then traveled the second half at twice the velocity of Synch. So there it would seem that it did not matter whether a spaceship traveled the whole spacetime interval at v or whether a spaceship waited and then accelerated to 2v. I was wondering why it would not make a difference there? I realize it is not as extreme example as you gave, but if what you were saying is correct, then I am slightly confused why the waiting and then going at a faster velocity did not matter in this example.

 

[Ibix]

It could also be considered from ShortnegX's frame of reference, where ShortposX passes it at 2v

That's not correct - look up relativistic velocity addition. Trivial example: What if v=0.8c? 2v=1.6c can't make sense.

ShortnegX was at rest for the time it took Synch to travel half the spacetime interval between event1 and event2

You've forgotten the relativity of simultaneity. The ShortposX/ShortnegX rockets' turnarounds are only simultaneous with Synch being halfway to the meetup in Synch's frame. In other frames they're not. You can see this in the triplet paradox setup on my Minkowski diagram page. Boost it to any frame you like - the only one where both turnarounds are on the horizontal axis (simultaneous with Synch's half-time) is Synch's rest frame.

 

[SlowThinker]

I realize it is not as extreme example as you gave, but if what you were saying is correct, then I am slightly confused why the waiting and then going at a faster velocity did not matter in this example.

Obviously Synch's clock will show more time than both ShortnegX and ShortposX (who will have equal times).

 

[name123]

You could use that as the basis of a coordinate system, although I think you'd need to be very careful about the details of how you specified it. And it could only cover the future and past light cones of event 1, not all of spacetime. And it wouldn't in general, correspond to any intuitive notion of simultaneity, and would be different from Einstein's notion of simultaneity.

I am not sure why that would be the case, because there could an event near the edge of the past light cone of event 1 for example, let's call it Event Past. There could then be an event in the future light cone of that event which was outside of the the past or future light cone of event 1. Let's call it Event Outside. I was thinking of the future light cone of event 1 to be the events event 1 could influence, and events in the past light cone of event 1 to be events which could have influenced it. Event Outside might not be influenced by or influence event 1 (spooky action at a distance aside), but it could presumably influence events in event 1's future light cone. Basically I was assuming events could be chained together.

But you don't need a definition of simultaneous for an event. It's when the clocks aren't currently at the same location that you need a definition of simultaneity. As I said, you could use the plane equidistant (equi-interval?) from event 1 as a plane of equal time coordinate, but I don't think it would be an inertial coordinate system, and it would be mathematically more complex for no particular gain.

Presumably the clock journey spacetime interval between event 1 would be what matters and not just the spacetime interval.

 

[name123]

Obviously Synch's clock will show more time than both ShortnegX and ShortposX (who will have equal times).

Ok, thanks. So the spacetime interval is the same for all, but the clock time depends on the velocities used to cross the spacetime interval. Symmetry in velocities symmetry on clock. Faster the velocities slower the clock. So from all three frames of reference the velocity Synch used to cross the spacetime interval was less than those of ShortnegX and ShortposX, so its clock ran faster and their's slower. So any claims by ShortnegX and ShortposX that Synch's clock was running slower would be wrong would they not?

Edit: I realize that I have made a mistake in considering stating "three frames of reference" because ShortnegX changes its frame of reference.

Edit 2: But observer ShortnegX would seem to be able to state:

a1 is the time passed on the clock of Synch during the first half of the spacetime interval.
a2 is the time passed on the clock of Synch during the second half of the spacetime interval.
b1 is the time passed on the clock of ShortnegX during the first half of the spacetime interval.
b2 is the time passed on the clock of ShortnegX during the second half of the spacetime interval.

i) a1 < b1
ii) a2 < b2
iii) a1 + a2 > b1 + b2

Yet all three being true seems to involve a logical contradiction.

Edit 3: I don't think I am using the edit convention in a standard way. There have been more edits than the post could be thought to indicate. I am now tending to use it to add new points, not to make clear where I edit to correct the way points are written. I have not always used it. So people making a response might quote stuff written in a different way from the way it appears in the post.

Edit 4: What I mean about what ShortnegX seems to be able to state is once ShortnegX makes certain assumptions and then takes the doppler effect into account.

Edit 5: Have I misunderstood?

Edit 6: I assume I would be thought to of have by believers in relative truth. Since they would presumably view it that while I was an observer during the first half of the space time interval, it was true, but then what was true when stated at event z became false when event z was in the past light cone and the velocity changed from when it was stated. Such that the truth of it was dependant on the velocity at a future time in which its truth was evaluated. Such that during the second half of the spacetime interval the truth of the statement changed.

 

[Ibix]

Basically I was assuming events could be chained together.

Not if you want to define simultaneous as equidistant from event 1. That implies the set of hyperbolic planes equidistant from event 1, and they're only space-like inside the light cone of event 1. Outside the light cone those equidistant planes are time-like, which is the very definition of not simultaneous.

You can patch together a global coordinate system from the joint lightcones of multiple events if you really want. You have to work out what to do in the regions where the light cones overlap. A systematic way of doing that is a complex procedure that really doesn't do much except disguise that you're just synching clocks in some sense.

Presumably the clock journey spacetime interval between event 1 would be what matters and not just the spacetime interval.

Between event 1 and what?

Yes, the path does matter. I was assuming inertial motion at a range of velocities in what I have written since #7.

 

[name123]

Yes, the path does matter. I was assuming inertial motion at a range of velocities in what I have written since #7.

I hadn't really understood earlier. I was thinking the spacetime interval could be used by itself to tell whether clocks would show the same time if they were synch'd at event 1 and then compared. I now understand that the velocities used to cross the spacetime interval matters. I assume that it would be possible to have standard velocity values for a standard spacetime interval, and that you could use these as components for the traveling of a spacetime interval, and if the values added up to the same, the clocks would be in synch. So if there was a symmetry in velocities the components would add up to the same and the clocks would be known to be in synch, but presumably even if the velocities were not symmetrical the components could be still be added up in order to tell.

Edit: I was just considering spacetime intervals in a single space dimension.

Edit2: I realize that two spacetime intervals cannot be compared like that because for example there could be 2 spaceships at rest with different inertial frames. Both could consider their clocks to be at rest for one of two spacetime intervals of equal length. It seems to me that it would work however for a case where two observers synched their clocks at one event, and then met up again at a later event. Have I still misunderstood?

 

[SlowThinker]

Edit2: I realize that two spacetime intervals cannot be compared like that because for example there could be 2 spaceships at rest with different inertial frames. Both could consider their clocks to be at rest for one of two spacetime intervals of equal length. It seems to me that it would work however for a case where two observers synched their clocks at one event, and then met up again at a later event. Have I still misunderstood?

You're describing basic twin paradox. Two ships cannot meet again if none of them accelerates. You'll need to describe who does what to meet again, to know what their clocks will show.
What's the trouble here? In basic twin paradox, the two ships (Earth and Traveller) meet at two events (start and finish) yet their clocks show different times. Nothing new here.

 

[Ibix]

I was thinking the spacetime interval could be used by itself to tell whether clocks would show the same time if they were synch'd at event 1 and then compared.

Compared how? If they meet up and compare clocks then the interval along each clock's route is exactly the information you need to work out what the clocks will read.

If they are not meeting up, then whether or not the clocks having the same time is simultaneous depends on your definition of simultaneous. You can use that condition to define simultaneous, but it won't correspond to any obvious definition of simultaneity in physical terms, where Einstein's definition does.

I now understand that the velocities used to cross the spacetime interval matters. I assume that it would be possible to have standard velocity values for a standard spacetime interval, and that you could use these as components for the traveling of a spacetime interval, and if the values added up to the same, the clocks would be in synch.

This makes no sense to me at all. Please look up Minkowski diagrams and learn to draw them. Intervals turn out to be closely related to the length of lines on the diagram (they're literally the lengths of lines in actual Minkowski space) and velocities are related to the angles between lines. So your first sentence I quoted above, in those terms, read that "the angles used to cross the lengths matters". Either you are not understanding something or I don't understand what you are trying to describe.

Have I still misunderstood?

I have no idea because I can't make head or tail of that paragraph. SlowThinker seems to think you are describing the twin paradox, but you seem to me to be contrasting two scenarios. Can you write down clearly what two cases you are trying to describe? What velocities do the ships have, when do they meet?

 

[Dale]

Please look up Minkowski diagrams and learn to draw them. Intervals turn out to be closely related to the length of lines on the diagram (they're literally the lengths of lines in actual Minkowski space) and velocities are related to the angles between lines.

@name123 I also highly recommend this approach. The spacetime interval is the Minkowski length of a line, and the relative velocity is an angle. Lines that are more vertical than light are called timelike and lines that are more horizontal are called spacelike. The coordinates are just arbitrary lines and don’t change any of the underlying geometry. In principle you could do physics without them although in practice they are very convenient.

 

[name123]

This makes no sense to me at all. Please look up Minkowski diagrams and learn to draw them. Intervals turn out to be closely related to the length of lines on the diagram (they're literally the lengths of lines in actual Minkowski space) and velocities are related to the angles between lines. So your first sentence I quoted above, in those terms, read that "the angles used to cross the lengths matters". Either you are not understanding something or I don't understand what you are trying to describe.

What I mean by:

I assume that it would be possible to have standard velocity values for a standard spacetime interval, and that you could use these as components for the traveling of a spacetime interval, and if the values added up to the same, the clocks would be in synch.

Is that I am assuming values could be given for velocities over a spacetime interval of a certain length. Let's call that length l and the "space interval velocity value" would be the value that the "interval function" i(v) returns.

So for example with the ShortnegX etc., example a spaceship called Synch can be considered to be at rest at event 1 with ShortnegX and ShortposX passing each other and synchronising their clocks (event 1) ShortnegX traveling in the -x direction at velocity -v and ShortposX traveling in the +x direction at velocity v (from Synch's perspective/frame of reference), for a spaceinterval of length 100l, and then both reversing direction and coming back to Synch (event 2). So the spacetime interval between the two events would be 200l and for ShortnegX the "space interval velocity value" would be 100 * i(-v) + 100 * i(v) and for ShortposX that value would be 100 * i(v) + 100 * i(v), whereas for Synch it would be 200 * i(0).

The same scenario could also be considered from ShortnegX's frame of reference, where at event 1 ShortposX passes it at 2v and Synch at v. ShortposX would then once having traveled a spacetime interval of 100l be considered to decelerate to rest and ShortnegX to accelerate to 2v and travel until it reached ShortposX (event 2). So for ShortnegX the "space interval velocity value" would be 100 * i(0) + 100 * i(2v) and for ShortposX that value would be 100 * i(2v) + 100 * i(0) and for Synch it would be 200 * i(v).

So I would then assume 200 * i(0) - ( 100 * i(-v) + 100 * i(v)) = 200 * i(v) - (100 * i(0) + 100 * i(2v)).

I was only assuming that this would be correct for two events in which observers met up at the first event and then met up again at the second.

Not sure whether it would be useful, it was just a consideration, which could perhaps highlight whether I had misunderstood. Thanks for everyone's patience given the amount of misunderstandings I have displayed so far.

 

[jbriggs444]

I am assuming values could be given for velocities over a spacetime interval of a certain length.

What does that even mean? The endpoints on spacetime intervals are events. They have fixed positions and fixed times. Given a straight-line path between two fixed endpoints at two fixed times there is no freedom to choose a velocity.

 

[Ibix]

I am assuming values could be given for velocities over a spacetime interval of a certain length. Let's call that length l and the "space interval velocity value" would be the value that the "interval function" i(v) returns.

Why assume? Why not look up the interval - it's hardly complex maths.

So for example with the ShortnegX etc., example a spaceship called Synch can be considered to be at rest at event 1 with ShortnegX and ShortposX passing each other and synchronising their clocks (event 1) ShortnegX traveling in the -x direction at velocity -v and ShortposX traveling in the +x direction at velocity v (from Synch's perspective/frame of reference), for a spaceinterval of length 100l, and then both reversing direction and coming back to Synch (event 2). So the spacetime interval between the two events would be 200l and for ShortnegX the "space interval velocity value" would be 100 * i(-v) + 100 * i(v) and for ShortposX that value would be 100 * i(v) + 100 * i(v), whereas for Synch it would be 200 * i(0).

This is wrong because you haven't looked up the definition of the interval, or haven't applied it if you have. You can indeed add the intervals from the two components of a ship's journey, but the results do not work the way you have written here.

where at event 1 ShortposX passes it at 2v

No it doesn't, as I said in #9.

The whole point of the interval is that it is invariant. You can calculate it in any frame, and the coordinates along the paths will be different, but the interval will be the same. So I think what you are trying to express is right, but interval doesn't work the way you've written it so it is difficult to know.

 

[Nugatory]

What does that even mean? The endpoints on spacetime intervals are events. They have fixed positions and fixed times. Given a straight-line path between two fixed endpoints at two fixed times there is no freedom to choose a velocity.

That statement could easily be misunderstand. If the two events are something like the beginning and end of a one-way journey to a distant location, the coordinate velocity is frame-dependent and can take on any value less than $c$, including zero. It's the four-velocity that is fixed.

 

[name123]

What does that even mean? The endpoints on spacetime intervals are events. They have fixed positions and fixed times. Given a straight-line path between two fixed endpoints at two fixed times there is no freedom to choose a velocity.

Maybe I had misunderstood. I had thought that given two events, one could go at a fixed velocity from one event to the other, or one could wait and then go. The longer you wait the faster you would need to go to get to the event, and going faster makes a difference to the clock times. Like in the example I gave where from ShortnegX's perspective, ShortnegX waited and then went at 2v, whereas Synch went at v the whole time. I was imagining that in such a situation the spacetime interval could be broken up into smaller spacetime intervals and values be worked out for appropriate for the proportion of mini spacetime intervals at the higher velocities. So consider two events in which there are ships at the location of event 1 which are at rest with a ship a distance away which is at the location of event 2. One ship could straight after event 1 accelerate to v and travel to event 2, and another could wait for half the spacetime interval at rest and then head at 2v to event 2, and another could wait 3/4 of the spacetime interval, and then head at 4v to event 2. I had assumed you could split the spacetime interval into 4 equal spacetime intervals, "mini intervals" if you like (and adding imaginary events if you like). I had assumed you could then then consider the ship at rest with event 2 to have been at rest for 4 mini intervals, the ship that waited 3/4 of the interval to have been at rest for 3 mini intervals and traveling at a velocity 4v for one, and the ship that waited 1/2 of the interval to have been at rest for 2 mini intervals and moving at 2v for two, and the ship that was at v the whole time to have been at v for all 4 mini intervals. I was thinking that the clocks could then be compared the one that had been at the event 2 location the whole time, and for each velocity 0, v, 2v, and 4v a value could be given equal to the clock difference divided by how many out of the 4 mini intervals a traveled at that velocity to create the time difference (if there was one). I realize I may have misunderstood.

 

[SlowThinker]

another could wait for half the spacetime interval at rest

First thing, you seem to be using the term "spacetime interval" inappropriately. The spacetime interval between 2 events that are $\Delta x$ light-seconds and $\Delta t$ seconds apart, is defined as $(\Delta t)^2-(\Delta x)^2$ (or a square root of that). It has the property that it's the same in all (inertial flat) coordinate systems.
You can wait time. You can't "wait" a spacetime interval, at least in the usual sense.

Second, the closest thing to that function $i(v)$ is probably the usual $\gamma$ factor $1/\sqrt{1-v^2/c^2}$. Although the math, as you suggested it, wouldn't quite work.

Third, what are you trying to do? Of course you can split the paths of the 5 spaceships into smaller parts, in fact you already did when you described the situation.
But what's your goal? You could define some 7 events in your scenario and compute their coordinates in any of the 5 or 9 reference frames, but other than being an exercise on Lorentz transformation, I don't see a point.
Or you may be trying to reinvent the special theory of relativity, in which case there are easier ways, in particular the parallel and perpendicular light clock.
Or you may be trying to gain some understanding, in which case I recommend the following scenario: there is a train track, with clocks every meter, all synchronized in the track's frame. Now you're in a train going on this track. How far apart will the clocks be? How fast will they run? What will the clock ahead and behind the train show? What happens to all these when the train starts or stops?
Or, is it something completely different? Why so many spaceships?

 

[vanhees71]

@name123 I also highly recommend this approach. The spacetime interval is the Minkowski length of a line, and the relative velocity is an angle. Lines that are more vertical than light are called timelike and lines that are more horizontal are called spacelike. The coordinates are just arbitrary lines and don’t change any of the underlying geometry. In principle you could do physics without them although in practice they are very convenient.

I've tried to write all this down here in as simple a way as possible (but not simpler):

https://th.physik.uni-frankfurt.de/~hees/pf-faq/srt.pdf

 

[sadovnik]

SRT, TIME, DIMENSIONS
a)
1905 - Einstein involved negative time in SRT
( nobody knew what negative time really was)
b)
1908 - Minkowski said that Einstein's equations look ''ugly''
And he gave beautiful mathematical solution changing
Einstein's ''ugly'' negative time into a positive time.
Minkowski explained his solution as a ''space-cone''
Today professors say to students:
''you cannot be physicists if you don't understand Minkowski's
beautiful mathematical solution''
( but nobody explains what ''space-cone'' or 4-D really is )
c)
Then in 1919 Kaluza and O.Klein involved 5-D
And in 1969 ''string''- physicists involved 11-D, 27-D, M-D
These super - D have never been observed, but physicists believe
that they are on the right way

You cannot do more complex arithmetic if you don't know what 2+2 = 4
and if you don't know what 4-D really is, then more complex dimensions
are only mathematical play for mathematicians
====
a) Classic view: dimension = direction
There are Descartes' three dimensions in space as
three directions in space. The point where all directions
are united shows place where object is.
We don't need more dimension, 3-D is enough to solve problem.
Looking on watch we know at what time object was in this point.

b) Minkowskki view:
there are four dimensions in space as four direction in space
but this ''space'' is not ordinary, it is very specific - '' an absolute spacetime''.
In this ''absolute spacetime'' we don't know the point and time
where object is exactly
=====

 

[Dale]

1905 - Einstein involved negative time in SRT
( nobody knew what negative time really was)

I don't think this is true.

Minkowski explained his solution as a ''space-cone''

This may be a language barrier. The usual term in English is "light cone".

but nobody explains what ''space-cone'' or 4-D really is

Yes, many people do.

but this ''space'' is not ordinary, it is very specific - '' an absolute spacetime''.

There is no need for it to be absolute spacetime, just spacetime is fine.

In this ''absolute spacetime'' we don't know the point and time
where object is exactly

Classically we can be exact.

 

[Ibix]

1905 - Einstein involved negative time in SRT
( nobody knew what negative time really was)

Negative time is totally non-mysterious and prosaic. We even use it in everyday speech - "ten minutes to five" is followed by "nine minutes to five" and so on. Did you mean negative time-squared in the definition of the interval $\Delta s^2=\Delta x^2+\Delta y^2+\Delta z^2-c^2\Delta t^2$?

1908 - Minkowski said that Einstein's equations look ''ugly''
And he gave beautiful mathematical solution changing
Einstein's ''ugly'' negative time into a positive time.

Again, I think you mean time-squared. The sign change is throughout (i.e. $\Delta s^2=c^2\Delta t^2-\Delta x^2-\Delta y^2-\Delta z^2$), and is purely a matter of whether you prefer your space-like intervals or your time-like intervals to have negative signs. Both conventions are in use today, often called "East Coast" and "West Coast" convention, and some care is needed to make sure you use a consistent convention. But consistency is the only thing that's important.

but nobody explains what ''space-cone'' or 4-D really is

I've never heard the term "space-cone". Can you provide a reference? Or did you mean "light-cone"? The meaning of that term would be defined in every single relativity textbook, I should imagine. And what four dimensions means is also clearly defined - for example chapter 2 of Carroll's lecture notes builds it up in painful detail from the notion of open sets.

Then in 1919 Kaluza and O.Klein involved 5-D
And in 1969 ''string''- physicists involved 11-D, 27-D, M-D
These super - D have never been observed, but physicists believe
that they are on the right way

Kaluza-Klein isn't necessary to explain electromagnetism, although it's one way of doing it. And string theory is still speculative. So I don't see your point.

You cannot do more complex arithmetic if you don't know what 2+2 = 4
and if you don't know what 4-D really is, then more complex dimensions
are only mathematical play for mathematicians

This is true. The implication, however, is that you believe that no-one knows what 4-D "really is". I gather that you don't, but please don't mistake "I personally do not know" for "no-one knows". Many people do.

Classic view: dimension = direction
There are Descartes' three dimensions in space as
three directions in space. The point where all directions
are united shows place where object is.
We don't need more dimension, 3-D is enough to solve problem.
Looking on watch we know at what time object was in this point.

I don't think this is exactly rigorous, but it's reasonable enough. You seem to be restricting yourself to discussing 3d manifolds, but don't seem to have realized that this is a self-imposed restriction. You can easily work in higher dimensional manifolds; then you have more than three dimensions.

b) Minkowskki view:
there are four dimensions in space as four direction in space

There are four dimensions in space-time, yes. What's conventionally called space is a 3d slice through space-time.

but this ''space'' is not ordinary

Formally, it's a 4d space with a Minkowski metric, as opposed to a Euclidean one. Whether you regard a 4d Euclidean space as ordinary is up to you.

'' an absolute spacetime''

I'm not sure what you mean by this term - can you provide a reference?

In this ''absolute spacetime'' we don't know the point and time
where object is exactly

Of course we do. However, as with Galilean relativity, there is more than one way to describe that point. In this sense, the only conceptual difference with Einsteinian relativity is that there is also more than one way to describe the time something happens as well as the place.

I have the impression that you have a very confused understanding of relativity, @sadovnik. I strongly suggest learning from a reliable source such as a textbook - Taylor and Wheeler's Spacetime Physics is such a source, and the first chapter is free to view online if you wish to try before you buy.

 

[name123]

First thing, you seem to be using the term "spacetime interval" inappropriately. The spacetime interval between 2 events that are $\Delta x$ light-seconds and $\Delta t$ seconds apart, is defined as $(\Delta t)^2-(\Delta x)^2$ (or a square root of that). It has the property that it's the same in all (inertial flat) coordinate systems.
You can wait time. You can't "wait" a spacetime interval, at least in the usual sense.

I simply meant be at 0 velocity for the spacetime interval. Or at least a spacetime interval of equal length.

Second, the closest thing to that function $i(v)$ is probably the usual $\gamma$ factor $1/\sqrt{1-v^2/c^2}$. Although the math, as you suggested it, wouldn't quite work.

In the post that you were responding to I did not mention the i(v) function specifically, but when I wrote:

I was thinking that the clocks could then be compared the one that had been at the event 2 location the whole time, and for each velocity 0, v, 2v, and 4v a value could be given equal to the clock difference divided by how many out of the 4 mini intervals a traveled at that velocity to create the time difference (if there was one).

I was explaining how I thought the i(v) function value could be calculated. I would not equal $\gamma$. So when you wrote "Although the math, as you suggested it wouldn't quite work", where you considering i(v) being gamma, and then considering how I was using it in post #18 wouldn't work, or were you suggesting that the way I was working it out in post #22 wouldn't work? If the latter could you explain why?

Third, what are you trying to do? Of course you can split the paths of the 5 spaceships into smaller parts, in fact you already did when you described the situation.
But what's your goal? You could define some 7 events in your scenario and compute their coordinates in any of the 5 or 9 reference frames, but other than being an exercise on Lorentz transformation, I don't see a point.

As I wrote in post #18

Not sure whether it would be useful, it was just a consideration, which could perhaps highlight whether I had misunderstood.

I had sometimes found myself getting confused with the idea of clocks going slower in different frames of reference, because it seemed to imply that less time would have expired, but what I kept overlooking was that with length contraction the spacetime interval would be invarient.

Or you may be trying to reinvent the special theory of relativity, in which case there are easier ways, in particular the parallel and perpendicular light clock.
Or you may be trying to gain some understanding, in which case I recommend the following scenario: there is a train track, with clocks every meter, all synchronized in the track's frame. Now you're in a train going on this track. How far apart will the clocks be? How fast will they run? What will the clock ahead and behind the train show? What happens to all these when the train starts or stops?
Or, is it something completely different? Why so many spaceships?

I was just doing it for understanding. With the train example, once it got to a higher velocity, I thought the clocks would appear to be less than a meter apart compared to a meter ruler on the train, and the clocks would appear to run slower. I had assumed that if the clock on the train was showing the same time as the clock on the track as it passes, and the train were a long one, and the clocks on the track were in synch (from train's frame of ref) as were the clocks on the track (from tracks frame of ref) that the clocks on the track in front of the train would appear to be further and further behind the display time of the clock on the train, and the clocks on the track behind the train would appear to be further and further ahead (the further back you went). But I assume I am wrong there. .

The reason I assume I am wrong is because supposing the track is 100000 light years long and the train is 1000 light years long. They synchronise their clocks, and it is agreed that the clocks are all in synch. The train then accelerates pretty much instantaneously to 0.6v for 1 second and then stops, what is the difference in time between the clock at the end of the train and the train on the track, and the clock at the front of the train and the clock on the track? And what were the observers on the front and end of the train considering the clocks opposite them on the track to be stating before the train stopped?

Clearly I still have some misunderstandings. Thanks for your patience and help.

 

[SlowThinker]

I simply meant be at 0 velocity for the spacetime interval. Or at least a spacetime interval of equal length.

Again, you can have zero velocity for some time but not for some spacetime interval.
You could adjust your speed so that you get from start to finish just by waiting, but that's not usually called "to wait a spacetime interval". (Note that it can only be done if the interval is positive, a.k.a. timelike.)

So when you wrote "Although the math, as you suggested it wouldn't quite work", where you considering i(v) being gamma, and then considering how I was using it in post #18 wouldn't work, or were you suggesting that the way I was working it out in post #22 wouldn't work? If the latter could you explain why?

As pointed out before, ShortposX doesn't pass ShortnegX at 2v but somewhat slower.

If ShortposX went at 2v for 1 year and then stopped for 1 year as viewed by ShortnegX, and ShortnegX stayed for 1 year and then went at 2v for 1 year, they would not end up at the same place.

I'm not saying the issues can't be fixed, but you'll end up reinventing the traditional special relativity.

With the train example, once it got to a higher velocity, I thought the clocks would appear to be less than a meter apart compared to a meter ruler on the train, and the clocks would appear to run slower. I had assumed that if the clock on the train was showing the same time as the clock on the track as it passes, and the train were a long one, and the clocks on the track were in synch (from train's frame of ref) as were the clocks on the track (from tracks frame of ref) that the clocks on the track in front of the train would appear to be further and further behind the display time of the clock on the train, and the clocks on the track behind the train would appear to be further and further ahead (the further back you went). But I assume I am wrong there.

If you replace the bolded "track" with "train", which is probably what you meant, then it sounds correct. Also I'd say that the clock in front show higher time, not lower, but that's a minor point here.
The point is that when the train starts to move, the track instantaneously shortens, and the clocks in front jump ahead and the clocks behind jump back. So you can't just say "moving clocks run slower", because they can also jump. (Note that if you factor in the light delay, you never see clocks go backwards or jump).

the train is 1 light year. They synchronise their clocks, the train accelerates pretty much instantaneously to 0.6v for 1 second and then stops, what is the difference in time between the clock at the end of the train and the train on the track, and the clock at the front of the train and the clock on the track? And what were the observers on the front and end of the train considering the clocks on the track to be stating before the train stopped?

Accelerating a long object is not simple. I'd just stick with a long track and a short train.

I'm not that familiar with SR but I'll try to show what I mean. Let's look at the moment the long train stops.
If it stops immediately in the train's frame, then seen from the track, the end will stop before the front, and the train will get spaghettified.
If it stops when the track's clock read 1s, then in the train's frame the front will start to brake first and the train gets crushed.
I'm not eally qualified to resolve this. I'd say during start, each of the wagons gets elongated by the pull of its neighbors to 1.25 original length, and if it survives, it will return to original length during slowdown. If it stops after 1s in track's frame, the clock all over the train will show $1/\gamma=0.8s$ after the 1s, so they will show 0.2s less than the track clock.

 

[Janus]

The reason I assume I am wrong is because supposing the track is 100000 light years long and the train is 1000 light years long. They synchronise their clocks, and it is agreed that the clocks are all in synch. The train then accelerates pretty much instantaneously to 0.6v for 1 second and then stops, what is the difference in time between the clock at the end of the train and the train on the track, and the clock at the front of the train and the clock on the track? And what were the observers on the front and end of the train considering the clocks opposite them on the track to be stating before the train stopped?

Once you apply acceleration to the train, all your careful synchronization of clocks goes out the window, Even observers in the train will no longer say that the clocks in the train are synchronized to each other anymore.

 

[Ebeb]

There are four dimensions in space-time, yes. What's conventionally called space is a 3d slice through space-time.

I recommend learning to draw Minkowski diagrams. That was the tool that finally showed me how simple all this stuff really is, even if it looks ridiculously complex at first glance.

Fully agree. Only math calculations will never give you the 4D insight.

-
Edit 2: link might be useful: http://ibises.org.uk/Minkowski.html

Good job, Ibix, but to fully understand those 3D cuts through 4D spacetime, the diagrams of your interactive Minkowski diagrams should also show the simultaneity line (3D slice through space-time) of the blue observer. Or dit I miss a button somewhere?

 

[Ibix]

Good job, Ibix, but to fully understand those 3D cuts through 4D spacetime, the diagrams of your interactive Minkowski diagrams should also show the simultaneity line (3D slice through space-time) of the blue observer. Or dit I miss a button somewhere?

Thanks - it was fun to write.

In any frame you can click "Keep axis" and the current x-t axes get added permanently to the diagram (change the Axis colour control to choose the colour). So you can boost to the outbound rest frame, add the axes, and reset to the stay-at-home frame.

Or you can add events that are simultaneous in the outbound frame and connect them manually (depends how precise you can be with a mouse).

Otherwise you have to write code to add another scenario including the simultaneity lines you want.

 

[Ebeb]

Thanks - it was fun to write.

In any frame you can click "Keep axis" and the current x-t axes get added permanently to the diagram (change the Axis colour control to choose the colour). So you can boost to the outbound rest frame, add the axes, and reset to the stay-at-home frame.

Or you can add events that are simultaneous in the outbound frame and connect them manually (depends how precise you can be with a mouse).

Otherwise you have to write code to add another scenario including the simultaneity lines you want.

O.K. I forgot that 'keep axis' button... :-(
But ... the axis line shows only half of the full simultaneity line/ 3D space cut (same remark for and time line). Even for the triplet paradox ...

 

[name123]

If ShortposX went at 2v for 1 year and then stopped for 1 year as viewed by ShortnegX, and ShortnegX stayed for 1 year and then went at 2v for 1 year, they would not end up at the same place.

Sorry for the delay in response by the way.

I assume you because you are considering that the length ShortposX had traveled would be length contracted from ShortnegX's perspective once it starts moving.

If you replace the bolded "track" with "train", which is probably what you meant, then it sounds correct. Also I'd say that the clock in front show higher time, not lower, but that's a minor point here.
The point is that when the train starts to move, the track instantaneously shortens, and the clocks in front jump ahead and the clocks behind jump back. So you can't just say "moving clocks run slower", because they can also jump. (Note that if you factor in the light delay, you never see clocks go backwards or jump).

Thanks I guess I should have checked, I was just assuming that the clocks in front would appear behind, so that when it stops, the ones opposite seemed to have ticked less. Unless I specifically state otherwise, I assume the light delay will have been factored in.

Accelerating a long object is not simple. I'd just stick with a long track and a short train.

I'm not that familiar with SR but I'll try to show what I mean. Let's look at the moment the long train stops.
If it stops immediately in the train's frame, then seen from the track, the end will stop before the front, and the train will get spaghettified.
If it stops when the track's clock read 1s, then in the train's frame the front will start to brake first and the train gets crushed.
I'm not eally qualified to resolve this. I'd say during start, each of the wagons gets elongated by the pull of its neighbors to 1.25 original length, and if it survives, it will return to original length during slowdown. If it stops after 1s in track's frame, the clock all over the train will show $1/\gamma=0.8s$ after the 1s, so they will show 0.2s less than the track clock.

What I was wondering is what at say 0.9 secs the clocks at either end of the long train would think the last clock on the track they passed had stated.

Regarding the clocks all over the train appearing slower than the ones on the track if it stopped. I don't quite understand. To highlight the point consider again the 2 long spaceships passing at 0.6v, both being long, say 10 light years each, and one passing through the middle of the other in a way analogous to a sausage roll. One spaceship being like the sausage one like the pastry. As a clock in the middle of the "sausage" spaceship roughly passes a clock in the middle of the "roll" spaceship , the clocks on each set themselves to zero and are synchronised on each (though not across spaceships). One can imagine the "pastry" ship being analogous to the track in the scenario you gave. The problem with the clocks all over the "sausage" spaceship showing 0.8 the amount of time that the clocks on the "pastry" spaceship showed, supposing 100 minutes had passed, that would seem to imply that the "sausage" spaceship clocks would be showing only 80 minutes had passed, if the "sausage" spaceship underwent an acceleration that placed it at rest with the "pastry" spaceship. But what if the "pastry" spaceship had undergone an acceleration that placed it at rest with the "sausage" spaceship?

 

[SlowThinker]

Regarding the clocks all over the train appearing slower than the ones on the track if it stopped. I don't quite understand.

There are 2 aspects to this: acceleration profile, and clock resynchronization.
1. You need to understand that it is different whether the train accelerates at once along its length in a) the original (track) frame, or b) in the moving frame. Assuming both acceleration and deceleration are simultaneous in the track frame, every car/sausage spent the same time moving, so the offset will be the same.
If it starts in the track frame but stops in the train frame, the front of the train will be moving longer and the clock will be more behind.
In your sausage spaceship, it's not clear which, if any of these 2 ways, you are imagining.

2. Let's say there is the driver in front and the conductor in the back. Just after acceleration, will the conductor think "hmm we should start moving any minute now" while the driver thinks "we've been moving for hours now"? Nope. Their clocks are simply out of sync, but they agree they've just started moving. If they stop soon, they don't need to bother resyncing their clocks in the moving frame.

You can compute the time elapsed on any of the clocks, but if they resynchronize, don't be surprised you get surprising/different results along the train/ship.

 

[name123]

There are 2 aspects to this: acceleration profile, and clock resynchronization.
1. You need to understand that it is different whether the train accelerates at once along its length in a) the original (track) frame, or b) in the moving frame. Assuming both acceleration and deceleration are simultaneous in the track frame, every car/sausage spent the same time moving, so the offset will be the same.
If it starts in the track frame but stops in the train frame, the front of the train will be moving longer and the clock will be more behind.
In your sausage spaceship, it's not clear which, if any of these 2 ways, you are imagining.

With the example I gave with the "sausage" spaceship and the "pastry" spaceship, there is only the acceleration to bring one of the spaceships into the rest frame of the other to compare clocks (after the 100 minutes on the clock of whichever spaceship undergoes the acceleration for example).

So It is not like the train example where the train undergoes 2 accelerations in different directions (one to accelerate and one to decelerate).

2. Let's say there is the driver in front and the conductor in the back. Just after acceleration, will the conductor think "hmm we should start moving any minute now" while the driver thinks "we've been moving for hours now"? Nope. Their clocks are simply out of sync, but they agree they've just started moving. If they stop soon, they don't need to bother resyncing their clocks in the moving frame.

You can compute the time elapsed on any of the clocks, but if they resynchronize, don't be surprised you get surprising/different results along the train/ship.

So in the "sausage" spaceship and the "pastry" spaceship example the clocks on each can be considered to be in synch, and both can calculate when they would be passing the designated clock on the other ship, and choose that time reset their clocks (along each spaceship). So one spaceship will reset their clocks at time x in their frame of reference, and the other will reset their clocks at time y in their frame of reference such that when the 2 appointed clocks pass they will see each others time as 0. Does the scenario now seem clear?

 

[jbriggs444]

With the example I gave with the "sausage" spaceship and the "pastry" spaceship, there is only the acceleration to bring one of the spaceships into the rest frame of the other to compare clocks (after the 100 minutes on the clock of whichever spaceship undergoes the acceleration for example).

Even if you accelerate only once, you will still mess up the clocks according to at least one of the frames involved.

 

[name123]

Even if you accelerate only once, you will still mess up the clocks according to at least one of the frames involved.

Yes, but the point is what would the clocks read if after 100 minutes after the reset according to the "sausage" spaceship, the "sausage" spaceship accelerated to the "pastry" spaceship frame of reference, and what would the clocks read if after 100 minutes after the reset according to the "sausage" spaceship, the "pastry" spaceship accelerated to the "sausage" spaceship frame of reference?

 

[Janus]

Sorry for the delay in response by the way.Regarding the clocks all over the train appearing slower than the ones on the track if it stopped. I don't quite understand. To highlight the point consider again the 2 long spaceships passing at 0.6v, both being long, say 10 light years each, and one passing through the middle of the other in a way analogous to a sausage roll. One spaceship being like the sausage one like the pastry. As a clock in the middle of the "sausage" spaceship roughly passes a clock in the middle of the "roll" spaceship , the clocks on each set themselves to zero and are synchronised on each (though not across spaceships). One can imagine the "pastry" ship being analogous to the track in the scenario you gave. The problem with the clocks all over the "sausage" spaceship showing 0.8 the amount of time that the clocks on the "pastry" spaceship showed, supposing 100 minutes had passed, that would seem to imply that the "sausage" spaceship clocks would be showing only 80 minutes had passed, if the "sausage" spaceship underwent an acceleration that placed it at rest with the "pastry" spaceship. But what if the "pastry" spaceship had undergone an acceleration that placed it at rest with the "sausage" spaceship?

Clocks according to "Sausage" and "Roll", according to each when their midpoints pass and each sync their clocks to zero.
Top is for the rest frame of the "sausage", bottom is for the rest frame of the "roll" . Thin cylinder is the sausage and thick transparent one is the roll. Numbers are rounded to the nearest 1/10.

A bit later, when the midpoint clock of the sausage meets the clock just to the left of midpoint ( as shown in the image). Again top is sausage frame, bottom is roll frame.

Sausage frame: Clock in roll starts 0.8 ly away, and thus takes 1.3333 yrs to reach the midpoint clock by the sausage clocks.. It ticks off 1.3333 x 0.8 = 1.06667 yr during that time. when it started it already read 0.6 years, thus it reads 1.6667 years upon arriving at the sausage midpoint.

Roll frame. Sausage midpoint clock starts reading zero and 0.8 ly away. It take 1.6667 years to reach the Roll's clock and ticks off 1.3333 years in doing so.

Thus both frame agree as to what the clocks read when they meet. This works out to be true for any pair of clocks.

As to what happens if either undergoes acceleration until they are at rest with respect to each other:
If the sausage undergoes acceleration, then It will measure the Roll as growing in length and its clocks as matching each other in synchronizing. It will measure its own clock as going out of sync with each other.
The roll will measure nothing happening to itself or its clocks, but will measure the sausage as growing in length and its clocks going even further out of sync. At the end both will agree that the roll clocks are in sync, while the Sausage clocks aren't. they also would both agree as to the respective readings of any two clocks that end up next to each other.

The reverse happens if it is the Roll that accelerates, the roll clocks will end up out of sync and the sausage clocks will be in sync.

The upshot is that which of the two undergoes the acceleration does make a difference in the outcome, but both will agree as to what that end result would be.

 

[SlowThinker]

With the example I gave with the "sausage" spaceship and the "pastry" spaceship, there is only the acceleration to bring one of the spaceships into the rest frame of the other to compare clocks

OK so if we ignore the tear/crush issues, the clock can be stopped during acceleration because the time spent accelerating is negligible.
In the scenario where the train goes for 1 track-second at 0.6c, the train clock will reach 0.8s wherever they are.
In the sausage/roll scenario, if the sausage's clock all over the ship before turnaround are showing the same time as viewed by its crew, they will be showing different times after turnaround. Even though they are showing the same time as before the turnaround.

So in the "sausage" spaceship and the "pastry" spaceship example the clocks on each can be considered to be in synch, and both can calculate when they would be passing the designated clock on the other ship, and choose that time reset their clocks (along each spaceship). So one spaceship will reset their clocks at time x in their frame of reference, and the other will reset their clocks at time y in their frame of reference such that when the 2 appointed clocks pass they will see each others time as 0. Does the scenario now seem clear?

Not sure. You can do it for one clock on each ship, but if you do it all along its length, the clock on the same ship will be showing different times.
If you only do it for the central clock and set others on each ship according to the central clock, you don't even need to accelerate the ships. You can simply make a photo of the sausage ship's clock through its windows from the roll ship, to see that they are off.

Can you repeat which issues seem unclear as of now?

 

[Dale]

I think I am going to go eat sausage for breakfast!

Edit: I toasted a croissant for a roll too. Yum!

 

[name123]

Sausage frame: Clock in roll starts 0.8 ly away, and thus takes 1.3333 yrs to reach the midpoint clock by the sausage clocks.. It ticks off 1.3333 x 0.8 = 1.06667 yr during that time. when it started it already read 0.6 years, thus it reads 1.6667 years upon arriving at the sausage midpoint.

Roll frame. Sausage midpoint clock starts reading zero and 0.8 ly away. It take 1.6667 years to reach the Roll's clock and ticks off 1.3333 years in doing so.

Thus both frame agree as to what the clocks read when they meet. This works out to be true for any pair of clocks.

Not sure why there is any asymmetry. In your second diagram why it appears different to the "sausage" than it does to the "roll".

As to what happens if either undergoes acceleration until they are at rest with respect to each other:
If the sausage undergoes acceleration, then It will measure the Roll as growing in length and its clocks as matching each other in synchronizing. It will measure its own clock as going out of sync with each other.
The roll will measure nothing happening to itself or its clocks, but will measure the sausage as growing in length and its clocks going even further out of sync. At the end both will agree that the roll clocks are in sync, while the Sausage clocks aren't. they also would both agree as to the respective readings of any two clocks that end up next to each other.

The reverse happens if it is the Roll that accelerates, the roll clocks will end up out of sync and the sausage clocks will be in sync.

The upshot is that which of the two undergoes the acceleration does make a difference in the outcome, but both will agree as to what that end result would be.

What about the two clocks that passed each other when both were 0. Will they show the same time, or will it matter which underwent the acceleration to be at rest with the other? If the latter then does the interval between when they were set to 0 and the acceleration?

Also with the earlier scenario where it was a track and a 10 light year long train where all the clocks are synchronised and then the train accelerates to then travel at 0.6v for one second then decelerates to be back at rest with the track. What would the observers on the front and end of the train be considering the clocks on the track to be stating before the train stopped?

 

[name123]

Not sure. You can do it for one clock on each ship, but if you do it all along its length, the clock on the same ship will be showing different times.
If you only do it for the central clock and set others on each ship according to the central clock, you don't even need to accelerate the ships. You can simply make a photo of the sausage ship's clock through its windows from the roll ship, to see that they are off.

Can you repeat which issues seem unclear as of now?

The scenario seems clear to me, but what I am not sure about is if the central clocks were coloured red and all other clocks green, then when the "sausage" ship's red clock shows 100 minutes, what will the other ship's red clock be showing according to the "sausage" ship, and if one of the ships then accelerates to the others frame of reference, what difference does it make to the time found to be on the "pastry" ship's red clock which one did the accelerating?

Edit: Also with the acceleration, it can be assumed whether with a train or a spaceship that they are made up of multiple linked segments each with their own engine or thrusters. So no need to imagine the effect of a single engine propagating over a long object.

 

[Janus]

Not sure why there is any asymmetry. In your second diagram why it appears different to the "sausage" than it does to the "roll".

Call the clock on the Roll B and the One on the sausage A. Both scenarios start when the midpoint clocks are adjacent and read zero.
So, in the sausage frame we start like the top diagram and end as the bottom diagram.

The distance between Clock A and B is the same as the distance between Clock B and the roll midpoint clock. This is 1 ly in the roll frame, but length contracted to 0.8 ly in the sausage frame As B moves to the left to meet with A, A advances 1.3 yrs and B advances 1.1 yrs.

In the roll frame:

We still start as the midpoint clocks meet and read zero. But now, the distance between A and B is the distance between B and the roll midpoint clock as measured in the Roll frame and is 1ly. As A moves to the left to meet up with A, it takes 1.7 yrs according to the clock in the Roll frame and The sausage clocks tick off 1.3 years in that same time.

What about the two clocks that passed each other when both were 0. Will they show the same time, or will it matter which underwent the acceleration to be at rest with the other? If the latter then does the interval between when they were set to 0 and the acceleration?

There are some specifics missing here that would allow for an answer. If two clocks are right next to each other when one of them accelerates, and the acceleration is high enough that they don't move significantly with respect to each other during the acceleration ( in other words they are still right next to each other after the acceleration) then they will have the same time on them before and after. (Of course there will always some[i/] small displacement during the accleration.)

Also with the earlier scenario where it was a track and a 10 light year long train where all the clocks are synchronised and then the train accelerates to then travel at 0.6v for one second then decelerates to be back at rest with the track. What would the observers on the front and end of the train be considering the clocks on the track to be stating before the train stopped?

Again, once you accelerate the train, all the clocks on the train will go out of sync with each other as measured by the train, as will the clocks on the tracks. A the moment before the deceleration starts, an observer on the train will measure clocks on the tracks in front of him as being ahead in terms of time of the clock he is beside and those behind him.
So let's say you are in the front of the train. At that moment, you and the train is at rest with respect to the tracks, and your clock reads zero as do all the clock on the train and all the clocks on the tracks. You accelerate over an infinitesimal period of time to 0.6 c, so that you clock and the clock you were next to on the tracks for all practical purposes still read zero and are still next to each other. The clocks behind you on the tracks will be now reading less than zero and those in front as reading greater than zero (you won't actually see this, because of light signal delay). The difference in clocks will be 0.6 s for every 0.8 light sec away from you that any clock is.
You keep this up for 1 sec by your clock, during which time the clocks on the tracks advance 0.8 sec. The clock that you pass after that 1 sec will read 1.25 sec. ( its will have advanced by 0.8 sec during your 1sec, but was already reading 0.45 sec at the beginning of your 1 sec. A clock 0.8 light sec ahead of you on the track will read 1.85 sec, while one behind you will read 0.65 sec. Other track clocks will differ depending on their position on the tracks.

 

[name123]

Call the clock on the Roll B and the One on the sausage A. Both scenarios start when the midpoint clocks are adjacent and read zero.
So, in the sausage frame we start like the top diagram and end as the bottom diagram.
View attachment 229259

The distance between Clock A and B is the same as the distance between Clock B and the roll midpoint clock. This is 1 ly in the roll frame, but length contracted to 0.8 ly in the sausage frame As B moves to the left to meet with A, A advances 1.3 yrs and B advances 1.1 yrs.

In the roll frame:
View attachment 229258

We still start as the midpoint clocks meet and read zero. But now, the distance between A and B is the distance between B and the roll midpoint clock as measured in the Roll frame and is 1ly. As A moves to the left to meet up with A, it takes 1.7 yrs according to the clock in the Roll frame and The sausage clocks tick off 1.3 years in that same time.

Still not getting it. The top of each of the diagrams seems symmetrical but the bottoms seem different, and I am not sure why given the symmetry of their top. It seems like you are suggesting it makes a difference which is the "sausage" and which is the "roll". Is that what you are suggesting?

There are some specifics missing here that would allow for an answer. If two clocks are right next to each other when one of them accelerates, and the acceleration is high enough that they don't move significantly with respect to each other during the acceleration ( in other words they are still right next to each other after the acceleration) then they will have the same time on them before and after. (Of course there will always some[i/] small displacement during the accleration.)

I am fine with the time dilation due to acceleration being proportional to the amount of time at a given acceleration thus as the time spent accelerating tends to 0 the time dilation due to it tends to 0. What I am not clear about is that if the central clocks were coloured red and all other clocks green, then when the "sausage" ship's red clock shows 100 minutes, what will the other ship's red clock be showing according to the "sausage" ship, and if one of the ships then accelerates to the others frame of reference, what difference does it make to the time found to be on the "pastry" ship's red clock which one did the accelerating?

Again, once you accelerate the train, all the clocks on the train will go out of sync with each other as measured by the train, as will the clocks on the tracks. A the moment before the deceleration starts, an observer on the train will measure clocks on the tracks in front of him as being ahead in terms of time of the clock he is beside and those behind him.
So let's say you are in the front of the train. At that moment, you and the train is at rest with respect to the tracks, and your clock reads zero as do all the clock on the train and all the clocks on the tracks. You accelerate over an infinitesimal period of time to 0.6 c, so that you clock and the clock you were next to on the tracks for all practical purposes still read zero and are still next to each other. The clocks behind you on the tracks will be now reading less than zero and those in front as reading greater than zero (you won't actually see this, because of light signal delay). The difference in clocks will be 0.6 s for every 0.8 light sec away from you that any clock is.
You keep this up for 1 sec by your clock, during which time the clocks on the tracks advance 0.8 sec. The clock that you pass after that 1 sec will read 1.25 sec. ( its will have advanced by 0.8 sec during your 1sec, but was already reading 0.45 sec at the beginning of your 1 sec. A clock 0.8 light sec ahead of you on the track will read 1.85 sec, while one behind you will read 0.65 sec. Other track clocks will differ depending on their position on the tracks.

Sorry still not quite clear, I could guess at the calculation but it would be useful if you did it (if you don't mind), with the
10 light year long train where all the clocks are synchronised and then the train accelerates to then travel at 0.6v for one second then decelerates to be back at rest with the track. What would the observers on the front and end of the train be considering the clocks on the track to be stating before the train stopped? The reason I ask is that it seems from your answer that the observer at the end of the train would be thinking that the clock on the track was showing a time prior to the clocks being set to 0. I perhaps have misunderstood.

Edit: Changed the last sentence from:

The reason I ask is that it seems from your answer that the observer at the end of the train would be thinking that the clock on the train was showing a time prior to the clocks being set to 0. I perhaps have misunderstood.

to:

The reason I ask is that it seems from your answer that the observer at the end of the train would be thinking that the clock on the track was showing a time prior to the clocks being set to 0. I perhaps have misunderstood.

 

[SlowThinker]

if the central clocks were coloured red and all other clocks green, then when the "sausage" ship's red clock shows 100 minutes, what will the other ship's red clock be showing according to the "sausage" ship

If the relative speed is 0.6c, it will show 80 minutes.

and if one of the ships then accelerates to the others frame of reference, what difference does it make to the time found to be on the "pastry" ship's red clock which one did the accelerating?

If the pastry ship accelerated to the sausage frame, and the process was quick enough, the clock will still show 80 minutes. The clock won't just skip time when you are next to it. It only happens in the distance.
If it was the Sausage accelerating, you'd have to first ask "according to the Pastry, what do their clock show when the Sausage clocks show 100 minutes?" It's not 80 minutes but 125.

Edit: Also with the acceleration, it can be assumed whether with a train or a spaceship that they are made up of multiple linked segments each with their own engine or thrusters. So no need to imagine the effect of a single engine propagating over a long object.

Even then the links can be fired at different times. In fact, they always will be fired at different times from someone's perspective.

 

[name123]

If the pastry ship accelerated to the sausage frame, and the process was quick enough, the clock will still show 80 minutes. The clock won't just skip time when you are next to it. It only happens in the distance.
If it was the Sausage accelerating, you'd have to first ask "according to the Pastry, what do their clock show when the Sausage clocks show 100 minutes?" It's not 80 minutes but 125.

So when the red clock on the "sausage" ship frame of reference is showing 100 there is a near instantaneous acceleration into one frame of reference or the other the time on the "pastry" ship red clock will vary from 80 minutes to 125 minutes depending on which did the accelerating.

I must admit I find this confusing.

Because say the clocks on the ship were separated by a distance of a light second each according to each ship's own frame of reference; the clock on the "pastry" ship that had last passed the "sausage" ship's red clock showing 100 minutes could be known as the "pastry" ship's blue clock. Presumably they would agree on the time each was showing as they passed. Likewise on the "sausage" ship the blue clock could be the clock that last passed the "pastry" ship's red clock before the acceleration (it would presumably, from the frame of reference the "sausage" ship, also be showing 100 minutes prior to acceleration). Presumably they would both agree on what respective time each was showing as they passed. From what you wrote I assume the red clock on the "pastry" ship would be showing 80 minutes as it passed the "sausage" ship's blue clock. Yet when the "sausage" ship near instantaneously accelerates to be at rest with the pastry ship, the "pastry" ship's red clock will not show 80 minutes but 125 minutes. Will the "sausage" ship's blue clock still be showing 100 minutes at that point? And how does the time on the "pastry" ship's red clock not seem to jump to the "sausage" ship's blue clock? As the "pastry" ship's red clock was passing the "sausage" ship's blue clock was it not be showing 80 minutes then as the "sausage" ships blue clock seemed to instantaneously accelerate into rest with it, the "pastry" ship's red clock time changed to showing 125 minutes?

Edit: I assume I have made a mistake here, and that from the "pastry" ships frame of reference, it's red clock would be showing 80 minutes, the "sausage" ship's blue clock would be showing 100 minutes, and the "sausage" ship's red clock would be showing something like 64 minutes and hadn't yet started the acceleration, and that by the time it did, the "pastry" ships red clock was showing 125 minutes.

 

[SlowThinker]

So when the red clock on the "sausage" ship frame of reference is showing 100 there is a near instantaneous acceleration into one frame of reference or the other the time on the "pastry" ship red clock will vary from 80 minutes to 125 minutes depending on which did the accelerating.

I must admit I find this confusing.

Yes. There is no "when". There is "as seen from Pastry when" and "as seen from Sausage when", and they're different, and it also depends on position.

The acceleration doesn't move the clock, it just moves the perspective.

 

[name123]

Yes. There is no "when". There is "as seen from Pastry when" and "as seen from Sausage when", and they're different, and it also depends on position.

The acceleration doesn't move the clock, it just moves the perspective.

So what about the situation where the "sausage" spaceship is at rest with the "pastry" spaceship, and they all synchronous their clocks and reset to 0, and then the "sausage" spaceship then accelerates to 0.6v for one second, and then accelerates back to the rest frame of the pastry spaceship.

You can imagine the "sausage" spaceship to be segmented, and for each segment to have its own rockets, and for them to start the moment the clocks reset to 0. Presumably the observers on the "pastry" spaceship will all agree the segments all set off at the same time. Would the observers on the "pastry" spaceship all agree the segments reached 0.6v at the same time? If so would they all agree what the clocks of those segments read when they reached it? Also after the "sausage" spaceship which we can assume is 10 light years long has been going (according to it's frame of reference) for one second what roughly would the observers on the front and end of it think the last "pastry" spaceship clock each had passed was showing on its clock (imagine the "pastry" spaceship to be considerably longer than the "sausage" one)?

 

[Janus]

Still not getting it. The top of each of the diagrams seems symmetrical but the bottoms seem different, and I am not sure why given the symmetry of their top. It seems like you are suggesting it makes a difference which is the "sausage" and which is the "roll". Is that what you are suggesting?

Each image is a set of diagrams showing two different times: When the "midpoint" clocks meet and both read zero, and then later when the "sausage" midpoint clock meets the next clock Left of the midpoint clock of the "pastry". So I don't see where you get any asymmetry begin the top and bottom diagrams in each image.
Maybe animations will help:
The pastry is the red line and its clocks are the red ones, blue represents the sausage and its clocks. Both the pastry and sausage measure their own clocks as being 1 ly apart and their clocks synchronized to each other. The starting moment in each animation is when two clocks, each reading zero pass each other. I'll limit the animation to just two clocks in each frame to keep things simpler.

First the pastry frame:

The rightmost clocks both start at zero. The sausage and its clocks move to the left at 0.6c until its rightmost clock aligns with the leftmost pastry clock. We pasuse to compare clocks. The sausage clocks are closer together than the pastry clocks because the pastry is length contracted. The left sausage clock reads 0.6 sec before the right one due to the relativity of simultaneity. (though this clock doesn't have an active roll in this situation.). Both sausage clocks tick 0.8 as fast as the pastry clocks due to time dilation.

Now the sausage frame. Note that we have not changed anything about the scenario, we are just switching the frame from which we are making the observations.

Both right clocks still start at zero. But in this frame, it is the pastry that is in motion (left to right), and undergoes length contraction and whose clocks undergo time dilation and are effected by the relativity of simultaneity. Thus the left pastry clock starts with a reading of 0.6 yrs, and starts only 0.8 ly from the right sausage clock.
Thus it only takes 1.33 yrs for the right sausage clock and left pastry clock to meet. During which time, the pastry clocks run at a rate 0.8 that of the sausage clocks and advance 1.07 years, and since the left pastry clock started at 0.6 years, it reads 1.67 years upon reaching the right sausage clock.

I am fine with the time dilation due to acceleration being proportional to the amount of time at a given acceleration thus as the time spent accelerating tends to 0 the time dilation due to it tends to 0. What I am not clear about is that if the central clocks were coloured red and all other clocks green, then when the "sausage" ship's red clock shows 100 minutes, what will the other ship's red clock be showing according to the "sausage" ship, and if one of the ships then accelerates to the others frame of reference, what difference does it make to the time found to be on the "pastry" ship's red clock which one did the accelerating?

After 100 minutes by the sausage clock, the pastry red clock will read 80 min. ( and be 60 light min away) according to the sausage. If The sausage clock then suddenly accelerates to come to rest with respect to the pastry, then the red pastry clock will jump to read 125 min, after they have come to rest with respect to each other.
If the sausage clock accelerates, first you have to decide "when" it accelerates. Does it accelerate when it reads 80 min and is 48 light min from the sausage clock ( and according to it, the sausage clock reads 64 min), or does it accelerate when the sausage clock read 100 minutes according to the pastry, and the pastry clock reads 125 min and is 75 light min from the sausage clock.
In the first case, it will still read 80 min after acceleration and the pastry clock will jump to 100 min.
In the second case, it will still read 125 min, and the sausage clock jumps to 156 min.

Sorry still not quite clear, I could guess at the calculation but it would be useful if you did it (if you don't mind), with the
10 light year long train where all the clocks are synchronised and then the train accelerates to then travel at 0.6v for one second then decelerates to be back at rest with the track. What would the observers on the front and end of the train be considering the clocks on the track to be stating before the train stopped? The reason I ask is that it seems from your answer that the observer at the end of the train would be thinking that the clock on the track was showing a time prior to the clocks being set to 0. I perhaps have misunderstood.

Edit: Changed the last sentence from:

The reason I ask is that it seems from your answer that the observer at the end of the train would be thinking that the clock on the train was showing a time prior to the clocks being set to 0. I perhaps have misunderstood.

to:

The reason I ask is that it seems from your answer that the observer at the end of the train would be thinking that the clock on the track was showing a time prior to the clocks being set to 0. I perhaps have misunderstood.

Whenever you start discussing acceleration and extended objects in relativity it can be very complicated. For example, there is something called the Rindler horizon, which limits what events an accelerating observer can measure in the direction opposite of his acceleration. The higher the acceleration, the closer to the observer, the Rindler horizon is. Now, In this scenario, where one is trying to limit the time of acceleration to an extremely short period, you have to assume an extremely high acceleration, and basically a Rindler horizon that, in effect, does not allow you to detect anything happening "behind" you.
To illustrate just how complex this subject is, here is a paper on the Rindler Horizon and its effects in different situations.
http://www.gregegan.net/SCIENCE/Rindler/RindlerHorizon.html

Now obviously, if the clocks weren't set and started from zero until the train started its initial acceleration, then the train observer would never say that they read less than zero. However, if we assume that the track clocks had been running in sync with each other and counting up from negative readings to zero until the train accelerated, then the train observer, could say that some given moment after it reached 0.6 relative to the tracks, that some of the track clocks had not yet read 0 (again taking to account the Rindler horizon)

In all honesty, I would forgo tying to examine scenarios which involve extended objects and acceleration until you have a much greater grasp on those which deal strictly with inertial motion. Adding accelerations at this point will not make things clearer.