ahmeeeeeeeeee
- 21
- 0
Hello ,
A Problem I found In a book , although I have the answer , I can't understand it
the problem is
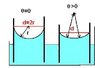
Calculate the force required to separate two glass plates of area 10 cm^2 each , with a film of water .5mm thick between them . take the coefficent of surface tention (T)to be 72 dyne/cm and theta = 0
The Answer written
since theta = 0 so the radius of curvature of the cylindrical surface between the plates is r = d/2 =.025 cm
((note : I Understand this but what If theta was another angle ??))
Delta P = T/r = 72/.025 = 2880 dyne/cm^2
the Normal force required = Delta P * Area = 2880*10 =2.88*10^4 dyne = .288 N #
I nead some explanation for this
Another _Identical problem_ says
two circular plates of radus 5 cm with 5 mm thick film of water betweem them , If the surface tention = 72.7*10^3 N/m , the normal force required to pull them Apart is what ?
it is the same I know , but in the solution ((the solution this time is not in the book , it is an assistant Engineer at the college)) said that :
Delta P = T(1/R1-1/R2) , R2 = infinity , so Delta P = T/R1
My problem is Why did he write a negative sign ?? I know it won't change the answer but why is it minus or it is just a writing error ??
A Problem I found In a book , although I have the answer , I can't understand it
the problem is
Calculate the force required to separate two glass plates of area 10 cm^2 each , with a film of water .5mm thick between them . take the coefficent of surface tention (T)to be 72 dyne/cm and theta = 0
The Answer written
since theta = 0 so the radius of curvature of the cylindrical surface between the plates is r = d/2 =.025 cm
((note : I Understand this but what If theta was another angle ??))
Delta P = T/r = 72/.025 = 2880 dyne/cm^2
the Normal force required = Delta P * Area = 2880*10 =2.88*10^4 dyne = .288 N #
I nead some explanation for this
Another _Identical problem_ says
two circular plates of radus 5 cm with 5 mm thick film of water betweem them , If the surface tention = 72.7*10^3 N/m , the normal force required to pull them Apart is what ?
it is the same I know , but in the solution ((the solution this time is not in the book , it is an assistant Engineer at the college)) said that :
Delta P = T(1/R1-1/R2) , R2 = infinity , so Delta P = T/R1
My problem is Why did he write a negative sign ?? I know it won't change the answer but why is it minus or it is just a writing error ??