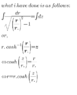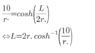The shape of the surface of a soap film

In summary, the differential equation for the film shape r(z) is given by cosh x. When the distance between rings is slowly increased, at a certain critical distance L•, the soap film breaks.
  • #1
Raihan amin
46
0
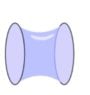
1. Two coaxial rings of radius R=10 cm are placed to a distance L from each other.There is a soap film connecting the two rings(that looks like a cylinder which have different radii with z coordinate. (The rings lie in xy plane)).Derive a differential equation describing the shape r(z) of the film where r is the radial distance from symmetry axis,as a function of distance z along the axis.
Show that cosh x is one of its solutions.
When the distance between rings is slowly increased ,at a certain critical distance L• ,the soap film breaks.Find L•
2.surface tension T=F/l and
Excess pressure inside a soap bubble is ∆P=4T/r3. I write the force balance equation for a divided part of soap film.
T.4Πr=∆P.Πr^2
and then
∆p=4T/r but I can't move ahead .Long hints is requested.
Thanks in advance.
 
Last edited by a moderator:
Physics news on Phys.org
  • #2
Can you please provide a schematic diagram of the system?
 
  • #3
I suppose the soap film surface . which is kind of the collateral surface of the cylinder with height L and radius R=10cm, can be described (in cylindrical coordinates) by ##r=r(z,\phi)## and I suppose it has symmetry with respect to ##\phi## so its just ##r(z)## as the exercise claims. I also suppose the soap film in the top and bottom surface of the cylinder can be taken to be flat or I don't know if we want for soap film to exist there. Still I can't be much of help for this problem never studied the laws of surface tension...
 
  • #4
Draw a catenoid type line (a string hanging loosely between two fixed points) connecting two points of the rings .it is the surface.
 
  • #5
So the axis of the rings is vertical and they share a common axis? You have a pressure difference in your equations. What is forcing this pressure difference? Is gravity a factor? Is the thickness of the film assumed uniform, or does it vary with z?
 
  • #6
They share a common axis .but as mass is not included i don't think gravity is a factor.and the question only says that r=r(z). To Illustrate the fig. I told you that the rings is in xy plane.
 

Attachments

  • IMG_20180914_202902_150.jpg
    IMG_20180914_202902_150.jpg
    3 KB · Views: 588
  • #7
OK. I’ll help you analyze this a little later when i’m back at my computer.
 
  • Like
Likes Raihan amin
  • #8
OK. We're going to be deriving a differential force balance on a small window shaped panel of film situated between ##\theta## and ##\theta + \Delta \theta## in the circumferential direction and between z and ##z+\Delta z## in the axial direction. This differential force balance will involve the unit vectors in the r, ##\theta##, and z directions and the derivatives of r with respect to z. For the window shaped panel of film that I have identified, what are

1. The lengths of the edges of the panel
2. The unit vectors within the plane of the film normal to the edges of the panel
 
  • #9
Can you show your work.
 
Last edited:
  • #10
Raihan amin said:
Can you sbow your work.
No. I'm expecting a response from you on my questions. If you don't understand what I'm asking, I'll be glad to help. But I need to see some effort on your part. That's how we do things on Physics Forums.

Chet
 
  • #11
There is a simpler way of doing this than the method I originally had in mind. Suppose we mathematically cut the film by hypothetical planes at z = 0 (the axial location of minimum radius ##r_0##, half way between the two rings) and the other at arbitrary z. The axial tensile force on the film at z = 0 will be in the negative z direction, and of magnitude ##2T(2\pi r_0)##, where T is the surface tension. What is the magnitude and direction of the axial tensile force on the film at the plane of arbitrary z, in terms of T, r, and the slope dr/dz?
 
  • Like
Likes Raihan amin and TSny
  • #12
T(z)=T(2πr)/[(1+r'²)½]; In the negative z direction.
Is it?
 
Last edited:
  • #13
Raihan amin said:
T(z)=T(2πr)/[(1+r'²)½]; In the negative z direction.
Is it?
Very close. There would be a factor of 2 out front to account for the surface tension at both the inner and outer interfaces of the film with the air; and, for the portion of the film between 0 and z, the tension exerted by the film at ##z^+## on the film at ##z^-## would be in the positive z direction.

So the overall force balance on the portion of the film between 0 and z would be:
$$\frac{2T(2\pi r)}{\sqrt{1+(\frac{dr}{dz})^2}}-2T(2\pi r_0)=0$$or$$\sqrt{1+\left(\frac{dr}{dz}\right)^2}=\frac{r}{r_0}$$
 
  • Like
Likes Raihan amin
  • #14
I got it.But it doesn't yield a cosh x like solution.is it?
 
Last edited:
  • #15
Raihan amin said:
I got it.But it doesn't yield a cosh x like solution.is it?
Have you tried to solve the differential equation for r as a function of z. Does ##r=r_0 \cosh(z/r_0)## satisfy the differential equation?
 
  • Like
Likes Delta2
  • #16
Now what to do?
 

Attachments

  • dz.png
    dz.png
    1.8 KB · Views: 622
  • #17
Raihan amin said:
Now what to do?
Look up the integral in a table of integrals.
 
  • #18
No. cosh x is not the solution of avove equation.
 
  • #20
How?
 
  • #21
See if the solution I posted in post #15 satisfies the equation.
 
  • Like
Likes Raihan amin
  • #22
OK.then how we will find L• ?
 
  • #23
I think this is correct.Now we have to find L•
 

Attachments

  • r(z).png
    r(z).png
    9.2 KB · Views: 631
  • #24
i just saw this thread
to find l you have to apply boundary conditions
 
  • #25
But we have only one boundary value
 
  • #26
The boundary condition is that at z = L/2 the radius must be 10cm with the centre of the soapbfilm having some ro after certain l there is no solution for ro and hence no film
 
Last edited:
  • #27
Can we find the highest L from that equation only?
 

Attachments

  • l.png
    l.png
    1.3 KB · Views: 409
  • #28
Yes but the form you behave written in seems a bit complicated let 1/r be X if 1/r has to have solution then X have to have solution
 
  • #29
Please carry out
 
  • #30
What
 
  • #31
I don't understand that.would you please do it for me?
 
  • #32
no i can't help you do it but
##
\frac {10}{r_0} = cosh(L/2 r_0)\\
\frac{1}{ r_0} = x\\

10 x = cosh (Lx /2)
##
now you can think of it graphically what is necessary for x to have solution
 
  • #33
Hi. I was trying to solve the same problem you submitted. And I've read Chestermiller's solution to the problem. But I don't understand why in the post #13 there is a sqrt(1+(dr/dz)^2)) ? I would appreciate the help. Thank you.
 
  • #34
LordGfcd said:
Hi. I was trying to solve the same problem you submitted. And I've read Chestermiller's solution to the problem. But I don't understand why in the post #13 there is a sqrt(1+(dr/dz)^2)) ? I would appreciate the help. Thank you.
The square root factor is associated with getting the z-component of the surface tension force.
 
  • #35
LordGfcd said:
Hi. I was trying to solve the same problem you submitted. And I've read Chestermiller's solution to the problem. But I don't understand why in the post #13 there is a sqrt(1+(dr/dz)^2)) ? I would appreciate the help. Thank you.
Let's see your derivation of the force balance on the film.
 
<h2> What causes a soap film to have a curved surface?</h2><p>The surface of a soap film is curved due to the surface tension of the soap solution. This surface tension is caused by the attraction between the soap molecules and the water molecules, which pulls the film into the smallest possible surface area.</p><h2> How does the shape of a soap film change when it is stretched?</h2><p>When a soap film is stretched, the surface tension decreases and the film becomes thinner. This results in a larger surface area and a flatter surface. If the stretching force is strong enough, the film can even break and form smaller droplets.</p><h2> Why do soap films have different colors?</h2><p>The colors seen on a soap film are the result of thin film interference. When light reflects off the top and bottom surfaces of the film, it interferes with itself and creates different colors depending on the thickness of the film. This is similar to the colors seen on a soap bubble.</p><h2> What factors affect the shape of a soap film?</h2><p>The shape of a soap film is affected by several factors, including the surface tension of the soap solution, the thickness of the film, and the stretching or bending forces applied to the film. Temperature and humidity can also play a role in the stability and shape of the film.</p><h2> Can the shape of a soap film be predicted mathematically?</h2><p>Yes, the shape of a soap film can be predicted using the Plateau-Rayleigh instability theory. This theory takes into account the surface tension, thickness, and boundary conditions of the film to determine its final shape. However, other factors such as external forces and imperfections can also affect the shape of the film.</p>

FAQ: The shape of the surface of a soap film

What causes a soap film to have a curved surface?

The surface of a soap film is curved due to the surface tension of the soap solution. This surface tension is caused by the attraction between the soap molecules and the water molecules, which pulls the film into the smallest possible surface area.

How does the shape of a soap film change when it is stretched?

When a soap film is stretched, the surface tension decreases and the film becomes thinner. This results in a larger surface area and a flatter surface. If the stretching force is strong enough, the film can even break and form smaller droplets.

Why do soap films have different colors?

The colors seen on a soap film are the result of thin film interference. When light reflects off the top and bottom surfaces of the film, it interferes with itself and creates different colors depending on the thickness of the film. This is similar to the colors seen on a soap bubble.

What factors affect the shape of a soap film?

The shape of a soap film is affected by several factors, including the surface tension of the soap solution, the thickness of the film, and the stretching or bending forces applied to the film. Temperature and humidity can also play a role in the stability and shape of the film.

Can the shape of a soap film be predicted mathematically?

Yes, the shape of a soap film can be predicted using the Plateau-Rayleigh instability theory. This theory takes into account the surface tension, thickness, and boundary conditions of the film to determine its final shape. However, other factors such as external forces and imperfections can also affect the shape of the film.

Similar threads

Effect of temperature on surface tension
Replies
2
Views
450
Surface Tension - Using hot soapy water to wash clothes
Replies
1
Views
2K
Shape of a bubble inside a rotating container
Replies
5
Views
2K
Force of a magnetized cylinder on a ferromagnetic surface
Replies
1
Views
2K
Rotating and tilting charged disk induces a voltage inside a ring
Replies
11
Views
2K
Surface Tension of a soap film
Replies
16
Views
5K
Understanding Surface Tension and the Role of Force in U-Shape Wire Frames
Replies
6
Views
3K
Soap bubbles sticking to each other
Replies
5
Views
4K
Tension in a deformed cylindrical bag on a surface
Replies
18
Views
717
Two soap bubbles coalesce, what is the surface tension?
Replies
4
Views
18K

Hot Threads

Recent Insights

Back
Top