chawki
- 504
- 0
Homework Statement
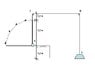
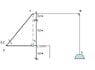
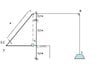
In the figure between AB is an upright rigid rod and flexible access to B from a rope which passes around the points C and D are located in the rollers for spot through the point E, where the rope is attached to weight.
Homework Equations
How much in section E, this weight will increase when the rod AB be translated into a horizontal plane
The Attempt at a Solution
I really don't get it..any hints?