How Does Torque Affect the Motion of a Disc Pulled Across a Table?

[ago01]

Homework Statement

A uniform cylindrical spool of string has radius R=3 cm, and mass M=500g. You accelerate the spool along a table by applying a constant force F=2N to the string. The spool rolls along the table without slipping and you can ignore the mass of the string. What is the acceleration of the center of mass of the spool? What is the magnitude of the static friction?

Relevant Equations

Torque, angular acceleration, force

I started out by drawing a diagram:

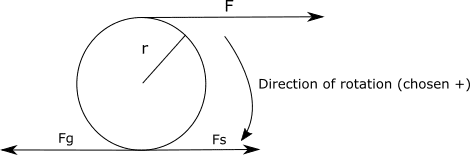
So I thought I would try torque with the axis of rotation in the center:

$T_1R = \frac{Mr^2}{2}\alpha$

and given that $T_1$ is equal to $F$ in the positive direction.

$\alpha = 266.6 \frac{rad}{s^2}$

Then knowing the relationship between angular acceleration and tangential acceleration:

$\alpha = \frac{a_t}{r}$
$a_t = \alpha*r$
$a_t = 7.998 \frac{m}{s^2}$

But this is not correct. The center of mass is translating and the rest of the object is rotating around it. $a_t$ would be the acceleration of a particle on the edge of the spool. Without this I cannot solve the second part so I am stuck.

So what if instead I just consider the translational portion?

$F_x = Ma$
$T_1 = Ma$
$T_1/M = a$
$a = 4 \frac{m}{s^2}$

But this is also incorrect. This would be like dragging the cylinder with slipping. It seems I am missing the connecting equations for rotational and translational motion.

 

[haruspex]

What does Fg represent?

Your first equation does not consider all the torques on the cylinder. Look again at your diagram.

 

[ago01]

What does Fg represent?

Your first equation does not consider all the torques on the cylinder. Look again at your diagram.

I finally got it with that hint.

For some reason I remember the professor in the video saying that in rolling motion static friction is the reason the object moves forward. Reviewing my book, the diagrams of a bicycle wheel only show a vector for static friction (like normal) opposite the direction of the force. I guess I manufactured a vector for no reason to represent the forward motion... it makes sense "static friction is the reason it moves" because the static friction applies additional torque:

$\sum{F_x} = T_1 - F_s$

$\sum{\unicode{x03A4}} = T_1R + F_sR = I\alpha$

Solving for $F_s$ in the first equation and plugging it into the second equation I get the answer.

But where I am confused still is - this is the tangential acceleration right (since we have $\alpha = \frac{a_t}{R}$)? How is this also the acceleration of the CM moving forward?

 

[PeroK]

But where I am confused still is - this is the tangential acceleration right (since we have $\alpha = \frac{a_t}{R}$)? How is this also the acceleration of the CM moving forward?

It can be seen from a combination of Newton's second and third laws. Internal forces cancel leaving the acceleration of the centre of mass to obey $F_{ext} = ma_{com}$.

Most mechanics textbooks should go through this calculation.