How Far Should the Rescue Crew Fly to Reach the Plane?

[COCoNuT]

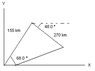
Emergency Landing. A plane leaves the airport in Galisto and flies a distance 155 km at an angle 68.0 Degrees east of north and then changes direction to fly a distance 270 km at an angle 48.0 degrees south of east, after which it makes an immediate emergency landing in a pasture.

1.) When the airport sends out a rescue crew, how far should this crew fly to go directly to this plane?

how do i find that? i included a picture that i THINK is correct.

 

[jamesrc]

The direction of the first leg of the trip is incorrect in your picture. It says 68 degrees east of north in the problem, but your picture shows 68 degrees north of east.

Once you've cleared that up, the law of cosines should help you find the length in question (first use your knowledge of geometry to determine the angle).

 

[COCoNuT]

am i trying to find the third leg? if so can't i do 155^2+270^2=C^2
C=311 .32

 

[jamesrc]

I'm afraid not. That would only work if this were a right triangle. You should find that the angle opposite the third leg is 110 degrees. The law of cosines goes like this:

c^2 = a^2 + b^2 - 2ab\cos\theta

where θ is the angle opposite side c.

 

[COCoNuT]

ah thanks alot. one more question...
In which direction? (Express your answer as an angle measured south of east).

how would i find out which direction it's going?