I How fast does a blastwave travel?

[Baluncore]

Especially as we now have the Friedlander equation that doesn't have any wave-like e{ix}, e{-ix} components.

Do not forget that; e^iz = cos(z) + i⋅sin(z)
https://en.wikipedia.org/wiki/Euler's_formula

 

[Squizzie]

Do not forget that; e^iz = cos(z) + i⋅sin(z)
https://en.wikipedia.org/wiki/Euler's_formula

Precisely, but Friedlender's equation has no i term!

 

[Baluncore]

The Friedlander equation is an approximation to the pressure of a blast wave. Blast waves do not follow the Friedlander equation as a law.

It seems that Friedlander simplifies the analysis by assuming the wave is damped to one cycle. It predicts the rarefaction, and we should expect the integral of the pressures above and below atmospheric pressure will be proportional.

 

[sophiecentaur]

The shockwave will lose speed as it travels

But will the wave maintain its profile until it slows to sonic speed. The 'wave' is surely more of a pulse which will disperse as soon as it's formed and you then have to ask which bit of the wavefront counts in the speed calculation?
If you observe a pulse, launched from a supersonic event, at various distances from its formation then is it not true that the pulse will spread out in time / distance? Can there be an answer to the OP question? I know that many people claim that the sonic boom they hear is actually a shock wave (don't ask for references) but PF has discussed this several times and my memory tells me that the wave acquires sonic speed very near the plane's path.

Any images of suitable graphs available?

 

[Baluncore]

If you observe a pulse, launched from a supersonic event, at various distances from its formation then is it not true that the pulse will spread out in time / distance?

The thing that defines a shock wave is that it is self-sharpening, as the higher pressure and temperature at the back of the pressure step, continuously catches up with the lower temperature at the front.

Once the compression and heating is sufficiently attenuated by inverse square law, the sharp step, falls to sonic velocity, and begins to take the form of a ramp, with attenuation of the high audio frequencies in the spectrum occurring more rapidly than the low.

By definition, the speed of an explosively generated shock-front is supersonic, due to the local heating in the front.

 

[hmmm27]

Once the compression and heating is sufficiently attenuated by inverse square law, the sharp step, falls to sonic velocity, and begins to take the form of a ramp, with attenuation of the high audio frequencies in the spectrum occurring more rapidly than the low.

I think the confusion is why form an (outwards) ramp. If it were an "ideal gas" all'round, without any of the normal variations in molecular velocity, would it stay a sharp step ? (gradually attenuating).

 

[Baluncore]

Sound waves are assumed to travel at sonic speeds, and do not assume heating of the air, during passage of the pressure wave.

If a pressure step increases the temperature, the pressure wave will be self-sharpening, with a supersonic speed.

There must be a transition defined between those two distinct models.

 

[Baluncore]

https://en.wikipedia.org/wiki/Rankine–Hugoniot_conditions

 

[sophiecentaur]

Once the compression and heating is sufficiently attenuated by inverse square law, the sharp step, falls to sonic velocity,

The inverse law must depend on the shape of the generating object - a sphere if it's an explosion but not for all shock waves. (Close to an aircraft or in a tube) This is hard stuff - that link of yours is not bed-time reading.

 

[Baluncore]

This is hard stuff - that link of yours is not bed-time reading.

The theory gets hard when you try to apply it to every possible case of supersonic flight, shock tube, and explosion.

If we can limit discussion to supersonic explosions, near the Earth's surface, then it can be discussed in this thread, without too much confusion.

 

[Squizzie]

@Baluncore I'm not sure that the Rankine–Hugoniot conditions (at least as summarised in Wiki) can be reconciled with the measurements reported in Kinney and Glasston.

 

[vanhees71]

But will the wave maintain its profile until it slows to sonic speed. The 'wave' is surely more of a pulse which will disperse as soon as it's formed and you then have to ask which bit of the wavefront counts in the speed calculation?
If you observe a pulse, launched from a supersonic event, at various distances from its formation then is it not true that the pulse will spread out in time / distance? Can there be an answer to the OP question? I know that many people claim that the sonic boom they hear is actually a shock wave (don't ask for references) but PF has discussed this several times and my memory tells me that the wave acquires sonic speed very near the plane's path.

Any images of suitable graphs available?

But also shock waves propagate with the speed of sound. What's moving with faster-than-sound speed is the source, which leads to the formation of the Mach cone.

 

[sophiecentaur]

But also shock waves propagate with the speed of sound. What's moving with faster-than-sound speed is the source, which leads to the formation of the Mach cone.

OK. So you connect a microphone to an oscilloscope. You display the sound of a sonic boom going past. Later, you record the microphone output using a loudspeaker source. Would you expect a different scope trace? Could you call what the loudspeaker produced a shock wave?

If you use a pair of microphones then the spacing of the two pulses will give an idea of a 'speed'. The wave front of the sound approaching the ground is tilted and the pulse spacing gives a supersonic 'virtual' speed? But that happens for all waves when you look from off the propagation axis. You can even measure an 'instant' / infinite speed when a stationary source is directly overhead the mid point of the microphones.

The pulse speed is the rate of actual energy transfer, normal to the wave front.

 

[Squizzie]

From the context of my OPs , where I referred to the Slo Mo Guys' C4 experiment and the Beirut explosion, I was clearly using the "term shock" wave to refer to what I now recognise is more appropriately described in the technical literature as a"blast wave" with a "shock front".

The subject of the shock wave generated by an object like a jet plane or a bullet travelling at a supersonic speed is a fascinating subject, but, as pointed out by @Drakkith at #39, it is a quite different physical phenomenon from that generated by an explosion.

Could I respectfully request @vanhees71 , @sophiecentaur , that we confine responses on this thread to the discussion of the blast wave/ shock front from an explosion and perhaps submit your thoughts about the shock wave from a plane or bullet on a separate thread. Unfortunately a brief search of PF indicates that earlier threads on the subject are mostly closed, so maybe you should start a new thread.

As I indicated in #71, I think there is a way to go on this one.

 

[sophiecentaur]

Could I respectfully request @vanhees71 , @sophiecentaur , that we confine responses on this thread to the discussion of the blast wave/ shock front from an explosion

Fair enough. I still have to ask when one should say the sound of an explosion is just a sound and not a shock front?
Near an explosion, is there a point where the ejecta is travelling at supersonic speed? Is this just a play on words and definitions. A detonation will carry with it, material that is more dense than the air it flies through so is it valid to talk in terms of gas laws and air temperature to set what we call the speed of sound.

There must be loads of data for videos of detonations in which at least a mean value for the speed of the 'blast wave' can be measured and also the speed of the 'bang' that's left over.

 

[Squizzie]

I still have to ask when one should say the sound of an explosion is just a sound and not a shock front?

And that's a very good question.

From rough estimations from the Slo Mo video it seems that the shock front is travelling at about the speed of the bullet (~Mach 1) when it impacts the target at the same time as the bullet, and from the Beirut explosion video, it appears to travel to the cameraman at around Mach 1 . So my feeling is that once it has departed the extreme temperatures of the explosion, it is a sound wave.

Normally, however, we associate the term sound wave with a sound that persists for a while: the note from a piano can be sustained over a period of seconds, and that of a violin, for as long as the bow is being drawn over the string. In the case of a blast wave, the duration of the sound of the blast wave: the bang! is of a very short duration (did you see Oppenheimer?)

But the duration of the blast wave is considerably longer - see videos of an atomic explosions, when the dust surges forward and back over a period of a few seconds.

So maybe the sound of the explosion is contained in the shock front, but blast wave, immediately behind the front, travelling at roughly the same speed as the shock front, can persist for a few seconds.

 

[berkeman]

From the context of my OPs , where I referred to the Slo Mo Guys' C4 experiment and the Beirut explosion, I was clearly using the "term shock" wave to refer to what I now recognise is more appropriately described in the technical literature as a"blast wave" with a "shock front".

The subject of the shock wave generated by an object like a jet plane or a bullet travelling at a supersonic speed is a fascinating subject, but, as pointed out by @Drakkith at #39, it is a quite different physical phenomenon from that generated by an explosion.

Could I respectfully request @vanhees71 , @sophiecentaur , that we confine responses on this thread to the discussion of the blast wave

Should I edit your thread title from "shockwave" to "blastwave"?

 

[Baluncore]

I'm not sure that the Rankine–Hugoniot conditions (at least as summarised in Wiki) can be reconciled with the measurements reported in Kinney and Glasston.

They are discussing the same subject.
Your lack of certainty, is your problem.

The Wiki page theory assumes that the temperature increase is significant, from which it follows that the speed of sound will increase as the wave front passes.

Kinney and Glasston were presenting the supersonic wave front velocity, from which they could estimate the momentary temperature rise of the shock front.

So my feeling is that once it has departed the extreme temperatures of the explosion, it is a sound wave.

If you can hear it, it is a sound wave. Feelings do not come into it.

We are discussing the step front wave that travels at greater than M 1.0

Any claim you make that the shock-front travels at exactly M 1.0 denies the thermal step that makes it special.

It remains a self-maintaining shock-wave until the velocity falls to M1.
The bandwidth of an audio recording system is clearly insufficient to reproduce the self-sharpening pressure step.

 

[sophiecentaur]

From rough estimations from the Slo Mo video it seems that the shock front is travelling at about the speed of the bullet (~Mach 1) when

You asked to restrict the discussion to detonations and you're back on flying objects. Which do you want?

Normally, however, we associate the term sound wave with a sound that persists for a while:

I don't. Our hearing has to deal with many percussive sounds, lasting for a few milliseconds. Do we make a distinction between that and your violin bow playing a minim length G? If I'm picky, I'd say that the speed of an endless note would be very hard to measure without some interruption / modulation as a marker. Kids measure the speed of sound by clapping their hands and counting the time for multiple echos from a wall.

So maybe the sound of the explosion is contained in the shock front, but blast wave, immediately behind the front, travelling at roughly the same speed as the shock front, can persist for a few seconds.

What you seem to be describing is the effect of dispersion. for a large source, a lot of air can be displaced and the resulting wave can travel a long way (across a town) and do damage (windows) at around 300m/s.

Alternatively, for very sub sonic speed. Did you ever see / own one of these?

 

[Squizzie]

Should I edit your thread title from "shockwave" to "blastwave"?

Yes, please.

 

[Squizzie]

You asked to restrict the discussion to detonations and you're back on flying objects. Which do you want?

I'm talking about the blast wave from the C4 explosion. I offer the trajectory of the bullet simply as a visualisation of the speed of sound.

 

[Baluncore]

I offer the trajectory of the bullet simply as a visualisation of the speed of sound.

The speed of a bullet is quite irrelevant to the speed of sound.

Some bullets are supersonic, at Mach 2.5, others are subsonic, at Mack 0.4

 

[Squizzie]

The speed of a bullet is quite irrelevant to the speed of sound.

Some bullets are supersonic, at Mach 2.5, others are subsonic, at Mack 0.4

In the case of the quoted video, the bullet is reported at 8:09 to be travelling at
387 m/sec which is Mach 1.1 in air at NTP.

 

[Squizzie]

Alternatively, for very sub sonic speed. Did you ever see / own one of these?

May refer you to my earlier post, requesting that discussion be constrained to explosive blast waves on this thread?
The air cannon is indeed a fascinating device, and the vortices it generates are an endless topic for discussion, but perhaps on a separate thread?

 

[Squizzie]

The bandwidth of an audio recording system is clearly insufficient to reproduce the self-sharpening pressure step.

Could I ask you to elaborate on "self-sharpening pressure step" please, and how it applies to blast waves?
I am not familiar with the term. A Google search comes up with pages about sharpening knives, ChatGPT doesn't recognise it but Bard provides :
"A self-sharpening pressure step is a type of pressure step that is used in adsorption processes to improve the separation of different components in a gas mixture."
so I'm not clear about what you are describing.

 

[sophiecentaur]

The air cannon is indeed a fascinating device, and the vortices it generates are an endless topic for discussion, but perhaps on a separate thread?

The relevance is the possibility of carrying 'destructive' power through the air, slowly.

 

[berkeman]

May refer you to my earlier post, requesting that discussion be constrained to explosive blast waves on this thread?
The air cannon is indeed a fascinating device, and the vortices it generates are an endless topic for discussion, but perhaps on a separate thread?

The relevance is the possibility of carrying 'destructive' power through the air, slowly.

If you folks want a separate discussion, please start a different thread. Thanks.

 

[Baluncore]

Could I ask you to elaborate on "self-sharpening pressure step" please, and how it applies to blast waves?

That is fundamental to the discussion here.
The speed of sound is proportional to the square root of temperature. So the speed of sound is faster in hotter air than colder air. The speed of sound is an immediate function of temperature, not of pressure.

The pressure wave generated by an explosion causes heating of the air.
The back of the shock-front is hotter than the front of the shock-front, so the back of the wave catches up with the front of the wave. That keeps the wave steep. I call that self-sharpening.

That pressure and temperature wavefront step will continue, until the compressive energy is no longer able to significantly heat the air. The speed will then be restricted to Mach 1, it will become a normal sound wave.

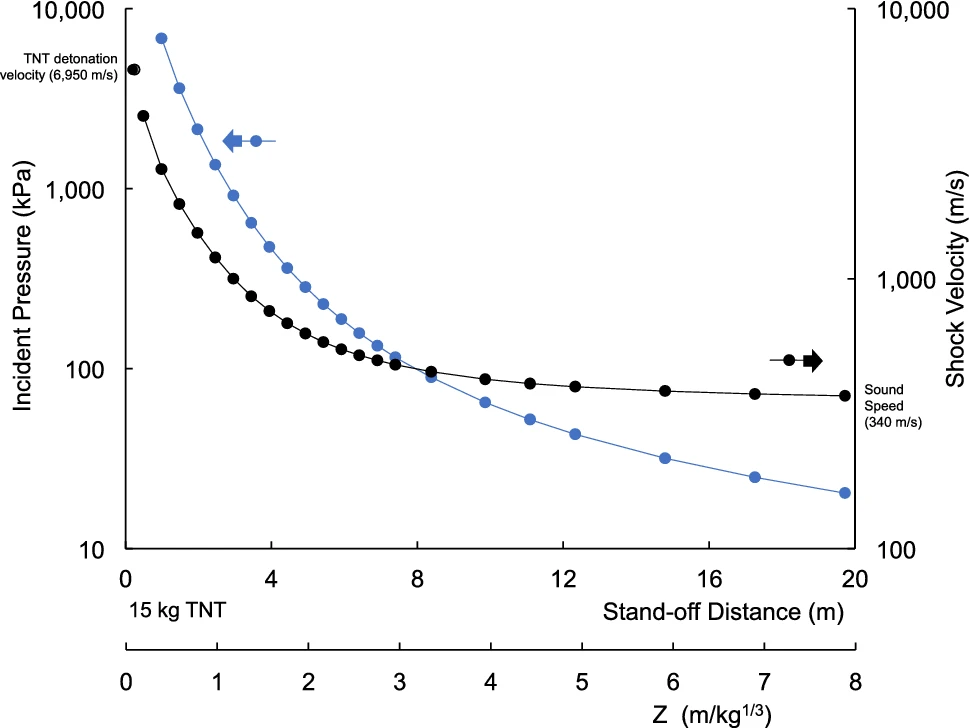
Look at table XI in Kinney and Graham. It shows that the velocity, Mx, of the shock-front, resulting from the detonation of 1 kg of TNT, is supersonic throughout the 500 metre passage of the blast wave.

Any supersonic blast wave must have a sufficient pressure step to cause a temperature rise, or it would not be supersonic.

Your persistent demands that, the shock-front of a blast wave must travel at the speed of sound, demonstrates a rejection of the fundamental step assumption that defines, and makes a shock-front special.

You are caught in a self-contradiction, a paradox of your own making. Once you understand the self-sharpening effect of the pressure step, you will understand what makes supersonic shock-fronts so interesting, and so destructive.

 

[Squizzie]

The back of the shock-front is hotter than the front of the shock-front, so the back of the wave catches up with the front of the wave. That keeps the wave steep. I call that self-sharpening.

But don't both Glasstone and Kinney suggest that, if anything, the back of the blast wave travels more slowly than the shock front, causing the back of the blast wave to lag further and further behind the shock front, rather than catch up as the blast wave travels away from the blast?

 

[Drakkith]

So maybe the sound of the explosion is contained in the shock front, but blast wave, immediately behind the front, travelling at roughly the same speed as the shock front, can persist for a few seconds.

This is all a bit vague and depends on what you mean by 'blast wave'. If we take a blast wave to be an explosively generated shock wave/front and the entirety of all of the effects seen as it passes by a region, then sure, it can last several seconds. I'd guess the sounds of a blast wave are generated mainly by the following (data taken from a 100g charge, so times may vary as the charge increases):

• The initial shock front, which, for small explosion sources at least, rises from ambient to peak pressure virtually instantly (much less than 1 ms).
• The decay of the shock front, which takes 3-4 ms.
• Sound waves generated by the interaction of the shock front with other objects as it passes.
• Vibrations induced in the audio equipment or your ear from the interaction of the shock front.
• Reflections of the shock front and other sound waves by terrain and local objects.

If you're far enough away not to have your eardrums or microphones blown out by the blast, then the end result should be a sharp crack as the shock front passes you followed by several seconds or more of induced and/or reflected sounds depending on the surrounding terrain. As the distance increases the sound should decay in amplitude and start to lose its high frequencies, ending up as a low-frequency 'rumble' that's often heard if you're very far away.

Reference for time values: https://www.mdpi.com/2076-3417/12/5/2691
Again, note that I don't know how the times change as explosive power increases. It could be that the durations increase, which is what I naively expect, but I don't know.

But will the wave maintain its profile until it slows to sonic speed. The 'wave' is surely more of a pulse which will disperse as soon as it's formed and you then have to ask which bit of the wavefront counts in the speed calculation?
If you observe a pulse, launched from a supersonic event, at various distances from its formation then is it not true that the pulse will spread out in time / distance? Can there be an answer to the OP question? I know that many people claim that the sonic boom they hear is actually a shock wave (don't ask for references) but PF has discussed this several times and my memory tells me that the wave acquires sonic speed very near the plane's path.

Any images of suitable graphs available?

Here's a graph of the pressure and velocity of a blast wave from 15 kg of TNT:

As you can see, after just 20 meters the blast wave has fallen from nearly 7,000 m/s to roughly the speed of sound at 340 m/s. Graph referenced from this article on Injury and death to armored passenger-vehicle occupants and ground personnel from explosive shock waves.