How does an observer moving at relativistic speeds perceive a pulsar?

[King Solomon]

TL;DR Summary

Let us suppose our velocity towards a distant neutron star roughly equated to a dilation factor of 10. On board our vessel we are equipped with a clock . Since the clock travels with us, it also experiences the same dilation; thus, in our frame, the clock keeps time the same as it did before we departed.

However, before we departed, we also had a second way to keep time: viz. The Pulses of the Neutron Star to which we are travelling. In our frame, the neutron star is now rotating 10x as fast.

Let us suppose our velocity towards a distant neutron star roughly equated to a dilation factor of 10. On board our vessel we are equipped with a NIST-F2 atomic clock . Since the clock travels with us, it also experiences the same dilation; thus, in our frame, the clock keeps time the same as it did before we departed.

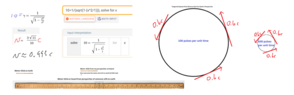
However, before we departed, we also had a second way to keep time: viz. The Pulses of the Neutron Star to which we are travelling. It was also observed, prior to departure that the surface of the neutron star was rotating at 0.6c (60% the speed of light).

In current our frame, the neutron star is now rotating 10x as fast, does this mean we would measure the rotation at 6c or at (1-[small number])c?I ask this question after watching the video:

Theoretical Physicist Brian Greene Explains Time in 5 Levels of Difficulty | WIRED"​

The idea of measuring time as contrast of two motions (neutron star pulses vs clock ticks) was considered the first level, the "Child Level." However, I don't think that we should so readily dismiss such a childlike notion of measuring time simultaneously with an on-board clock whose tick rate decreases with the Lorentz factor from the perspective of an observer that remained on earth.

 

[Ibix]

I'm not watching a haf hour video on a topic I already understand. It's easy enough to work out the pulse rate you receive as measured by your clock; it's just the relativistic Doppler factor, which includes the changing distance and the time dilation effect.

What did you want to discuss about this? If you're going to refer to the video please give specific time codes.

 

[PeterDonis]

Let us suppose our velocity towards a distant neutron star roughly equated to a dilation factor of 10.

If you are asking about what we actually see, with our eyes or through our telescopes, the relevant quantity is not the time dilation factor but the Doppler factor. For a time dilation factor of 10, the relativistic Doppler factor will be about 20 (the general formula is $D = \gamma \left( 1 + v \right)$ where $\gamma$ is the time dilation factor, $D$ is the Doppler factor, and $v$ is the relative velocity directly towards the object--note that for motion not directly towards the object the formula becomes more complicated).

It was also observed, prior to departure that the surface of the neutron star was rotating at 0.6c (60% the speed of light).

This is not a good way to characterize it, because this "velocity" is a coordinate velocity and will not necessarily be less than the speed of light when you transform between frames, so it's not clear what its actual physical meaning is. A better way to think of it is the frequency of the pulses from the neutron star (assuming it's a pulsar, meaning once every revolution it emits a pulse of radio waves in your direction). The frequency of the pulses will increase by the Doppler factor if you move at speed $v$ towards the pulsar, compared to the case where you are at rest relative to the pulsar.

 

[PeterDonis]

I ask this question after watching the video

Pop science videos, even by well-known physicists, are not good sources if you actually want to learn the underlying science. In this particular case, the math is pretty simple so it's fairly easy to learn the underlying science.

 

[King Solomon]

Pop science videos, even by well-known physicists, are not good sources if you actually want to learn the underlying science. In this particular case, the math is pretty simple so it's fairly easy to learn the underlying science.

Great, since it's so easy, what's the answer? What speed of rotation will be observed for the neutron star?

I keep getting the original answer, which is 0.6c, due to both time and space dilation (that is, the rotation rate remains constant, since my unit of length is also dilated).

 

[PeterDonis]

since it's so easy, what's the answer? What speed of rotation will be observed for the neutron star?

Go read the last part of my post #3 again.

I keep getting the original answer

Based on what calculation? I see no math anywhere in your post.

 

[Nugatory]

Great, since it's so easy, what's the answer? What speed of rotation will be observed for the neutron star?

The answer to that is, as @PeterDonis said, already in his post #3 of this thread.

I keep getting the original answer, which is 0.6c, due to both time and space dilation (that is, the rotation rate remains constant, since my unit of length is also dilated).

This problem is interesting enough you may want to work out for yourself why that $D = \gamma \left( 1 + v \right)$formula works. It's easiest to work with the frame in which the you and the ship are at rest and the pulsar is moving towards you at speed $v$. The pulsar emits a flash of light in your direction every $T$ seconds in its rest frame, the time dilation formula gives you the time between emission events using the frame in which you are at rest. That's not the time between when the flashes reach you though, because the pulsar is moving towards you so every successive flash covers a shorter distance and spends less time in flight before it reaches you.

Try it, it's actually sort of fun to really see how it works - and if you hit a hard spot either googling for "relativistic doppler" or posting your work here and asking for help will get you over it.

 

[PeterDonis]

the rotation rate remains constant, since my unit of length is also dilated

First, your unit of length is contracted, not dilated; and second, it's only contracted along the direction of relative motion, but the rotation of the neutron star is not purely in the direction of relative motion. So it can't possibly be as simple as you describe in this quote.

And third, the frequency of pulses, as I have already said, is increased by the Doppler factor, which is 20; and that must also be the frequency at which a particular point on the surface of the neutron star passes directly across your line of sight. Which would seem to indicate that the rotation rate, which is a frequency, will also be increased by a factor of 20.

And fourth, what that means for the rotation speed, as a coordinate speed in your rest frame, is a different question. You would not expect this coordinate speed to be constant, since different parts of the star are moving in different directions relative to you. You would also, as I've already said, have to ask yourself what the physical meaning of this coordinate speed is.

 

[King Solomon]

Go read the last part of my post #3 again.Based on what calculation? I see no math anywhere in your post.

In others words, I keep returning 0.6c.

 

[PeterDonis]

@King Solomon, math needs to be posted as LaTeX directly in the post, not as an image. Still less as an image that is not even an argument for anything, since you just plug numbers blindly into the time dilation formula without making any argument for why that's the correct formula for what you are trying to calculate. Since you have already been given an argument for why it is not, you can't just help yourself to the claim that it is.

 

[King Solomon]

@King Solomon, math needs to be posted as LaTeX directly in the post, not as an image. Still less as an image that is not even an argument for anything, since you just plug numbers blindly into the time dilation formula without making any argument for why that's the correct formula for what you are trying to calculate. Since you have already been given an argument for why it is not, you can't just help yourself to the claim that it is.

I'm not helping myself to the claim.

I know its wrong.

Can you please do me a favor, and show what the correct formulation is.

 

[PeterDonis]

Can you please do me a favor, and show what the correct formulation is.

I already did. Go read my post #3 again.

 

[King Solomon]

That is, as @PeterDonis says, in post #3 of this thread.This problem is interesting enough you may want to work out for yourself why that $D = \gamma \left( 1 + v \right)$formula works. It's easiest to work with the frame in which the you and the ship are at rest and the pulsar is moving towards you at speed $v$. The pulsar emits a flash of light in your direction every $T$ seconds in its rest frame, the time dilation formula gives you the time between emission events using the frame in which you are at rest. That's not the time between when the flashes reach you though, because the pulsar is moving towards you so every successive flash covers a shorter distance and spends less time in flight before it reaches you.

Try it, it's actually sort of fun to really see how it works - and if you hit a hard spot either googling for "relativistic doppler" or posting your work here and asking for help will get you over it.

I'm going to check it out and see if I get something other than 0.6c

Also, I assume I'm going to need a relativistic formulation of angular momentum as well, I will have to hold the axis parallel to the direction between the observer and the pulsar to trivialize one of the conditions (that is, with either the north or south pole of the pulsar facing us directly).

 

[Nugatory]

Also, I assume I'm going to need a relativistic formulation of angular momentum as well,

You don't need that - and a good thing too because it would make everything a lot harder.

We get flashed by the pulsar once every rotation when its beam is pointed directly at us and we don't care where the beam is going when it's not pointed at us. So all we need is the time interval between successive emissions in our direction, and that is much easier to model.

(And I'll repeat wat I said earlier - this problem is much easier to work using the frame in whoich we are at rest and the pulsar is approaching us).

 

[King Solomon]

You don't need that - and a good thing too because it would make everything a lot harder.

We get flashed by the pulsar once every rotation when its beam is pointed directly at us and we don't care where the beam is going when it's not pointed at us. So all we need is the time interval between successive emissions in our direction, and that is much easier to model.

(And I'll repeat wat I said earlier - this problem is much easier to work using the frame in whoich we are at rest and the pulsar is approaching us).

Here is Overleaf link in latex)
https://www.overleaf.com/read/jczpfyqtrffm

A neutron star pulses 100 times per second from earth, we then move towards it at 0.995 times the speed of light. How many times does the neutron star pulse in the moving frame.

Also, neutron star is rotating at 0.6 times the speed of light perpendicular to our line of sight. We then move at 0.995 the speed of light towards the neutron star. What speed will we measure the neutron star rotating at?

Since the velocities are orthogonal the relativistic addition formula reduces to:

$$V=\sqrt{\frac{v_1^2+v_2^2}{1+\frac{v_1v_2}{c^2}}}$$

Where, 0.6=$v_1$ is tangential velocity at any location on neutron star's equator when measured from Earth; 0.995=$v_2$ is velocity of the observer relative to the reference frame and $V$ will be observed tangential velocity from the perspective of the observer traveling at 0.995c.

From this we yield:

$$0.919c=V=\sqrt{\frac{0.6^2+0.995^2}{1+\frac{(0.6)(.95)}{1}}}$$

For the case of the number of pulses (I still do not see how the Relativistic Doppler Effect plays into this), we have a time dilation factor, $\lambda$, equal to 10.012

$$10.012=\lambda=\sqrt{\frac{1}{1+\frac{v_2^2}{1}}}$$

Which means we should observe $100/10.012$ pulses per second, which is 9.987 pulses for second.

Yet the increase from $v_1$ to $V$, viz. 0.6c to 0.919c, would imply to me that we should be observing 153.166 pulses per second.
Clearly the Relativistic Doppler effect mentioned by @PeterDonis should resolve this major discrepancy. But I still don't see how to apply it.

On the bright side, I'm getting $V$=0.919c instead of 0.6c, which I assume is correct.

 

[PeterDonis]

A neutron star pulses 100 times per second from earth, we then move towards it at 0.995 times the speed of light. How many times does the neutron star pulse in the moving frame.

Already answered in post #3.

neutron star is rotating at 0.6 times the speed of light perpendicular to our line of sight

This makes no sense. A rotation rate is a frequency, not a speed. The direction of motion of a particular point on a rotating object will be different for different parts of the object.

Clearly the Relativistic Doppler effect mentioned by @PeterDonis should resolve this major discrepancy.

What part of post #3 did you not understand? It's very simple: the Doppler factor is 20, so the frequency of pulses as observed by the moving observer is 20 times the frequency observed by the observer at rest relative to the neutron star. So if the latter is 100 times per second, the former will be 2000 times per second.

As for the "discrepancy", your calculations of "speed" are nonsense, as far as I can see, because you are treating the "rotation rate" as a speed, incorrectly, as explained above. Either you need to treat it as a frequency, or you need to do a separate calculation for different points on the neutron star's surface since their direction of motion relative to the moving observer will be different.

 

[PeterDonis]

How many times does the neutron star pulse in the moving frame.

Note that, as I said in post #3, the Doppler factor tells you the change in the frequency as actually observed by the moving observer, i.e., what they see with their eyes or through their telescope. As @Nugatory explains in post #7, this can, conceptually, be decomposed into two effects: the time dilation effect and the effect of the distance the light signals from the pulsar have to travel decreasing as the pulsar and the observer move towards each other. But I personally think it's better to focus on the actual observation since that's a direct measurement.

 

[Ibix]

@King Solomon -are you saying that (if we treat a pulsar as a rigid sphere) the velocity of a point on its equator in its rest frame is 0.6c? If so, you can compute what this velocity is in a frame where the pulsar is doing 0.995c if you like although, as Peter has stated several times, it is no longer a constant around the equator so your single number cannot be correct except for at most two points. So it's not really relevant to the observed pulse rate, which would be related to the average speed and the distance along the cycloid path traced out by the point in this frame (that's why comparing your instantaneous speed to the 0.6c isn't giving you the same factor of 20 Peter gets - you are using the wrong speed and the wrong distance). It's much easier just to use the relativistic Doppler factor$$\sqrt{\frac{c+v}{c-v}}$$since you are receiving a series of pulses with a known frequency and you just want to know the Doppler shift in that frequency.

 

[King Solomon]

@King Solomon -are you saying that (if we treat a pulsar as a rigid sphere) the velocity of a point on its equator in its rest frame is 0.6c? If so, you can compute what this velocity is in a frame where the pulsar is doing 0.995c if you like although, as Peter has stated several times, it is no longer a constant around the equator so your single number cannot be correct except for at most two points. So it's not really relevant to the observed pulse rate, which would be related to the average speed and the distance along the cycloid path traced out by the point in this frame (that's why comparing your instantaneous speed to the 0.6c isn't giving you the same factor of 20 Peter gets - you are using the wrong speed and the wrong distance). It's much easier just to use the relativistic Doppler factor$$\sqrt{\frac{c+v}{c-v}}$$since you are receiving a series of pulses with a known frequency and you just want to know the Doppler shift in that frequency.

The problem is conceptualizing what that means.

Suppose there is no significant change in velocity between the frame of the observer and the neutron star. We then observe an acceleration in the pulses from 100 times per second to 2000 times per second. This could only happen if the radius of the neutron star contracted, rotating at a superluminal speed to resist collapse (as it would now be smaller than its Schwarzschild radius).

Since the above cannot happen, and since the rate of neutron star pulses is the rate of rotation, there has to be a mechanism in play that prevents such an absurd behavior.

If am now traveling at this neutron star at 0.995c, and the pulse rate is now 20 times greater, and the neutron star experiences no length contraction in the plane perpendicular to my line of sight, then I would be observing superluminal rotation speeds of the neutron star from my rest frame. This again, cannot be possible.

So what is it that I'm missing here?

 

[PeterDonis]

The problem is conceptualizing what that means.

I already explained what it means in post #3. Have you read it?

Suppose there is no significant change in velocity between the frame of the observer and the neutron star.

Then you're changing the scenario, and this....

We then observe an acceleration in the pulses from 100 times per second to 2000 times per second.

...would not happen.

the rate of neutron star pulses is twice the rate of rotation

What? Where are you getting this from?

If am now traveling at this neutron star at 0.995c, and the pulse rate is now 20 times greater, and the neutron star experiences no length contraction in the plane perpendicular to my line of sight, then I would be observing superluminal rotation speeds of the neutron star from my rest frame.

No, you wouldn't. You would be calculating different relative speeds (speeds relative to you) for different points on the neutron star's surface (because they are moving in different directions relative to you), but none of those speeds would be superluminal. All of them are results of the relativistic velocity addition formula (the general vector formula that accounts for motion in different directions), and that formula can never give you superluminal speeds starting from subluminal speeds.

Also, relating these calculated speeds to the observed pulse frequency that is 20 times higher is not at all simple, since, as has already been pointed out, it involves both the time dilation factor and the shortening light travel time between you and the pulsar as you approach each other.

 

[King Solomon]

So you're claiming that the time between pulsar's emission is not equal to time between the neutron star's very own rotation?

Each rotation of the neutron star is one pulse.

Yet the Relativistic Doppler effect is compacting 20 pulses into the same time interval when travelling at 0.995c towards the neutron star.

There is no length contraction any direction perpendicular to the direction of motion, so the radius of the neutron star remains the same. So if the axis of rotation from the neutron is parallel to the direction of motion, then I have something rotating at incredible speeds (with a tangential velocity far greater than 0.6c, which the relativistic vector addition return a tangential velocity with a speed of 0.91c).

Perhaps a relativistic form of Cherenkov radiation can resolve this?

 

[Ibix]

So what is it that I'm missing here?

The Doppler effect, I think. I'm not sure what you're trying to say.

Remember that the neutron star is doing 0.995c, right behind the pulses it emits. So the pulses it emits are crowded up when you receive them. That's where the frequency increase comes from.

 

[PeterDonis]

So you're claiming that the time between pulsar's emission is not equal to time between the neutron star's very own rotation?

I have said no such thing. I am assuming that a pulse is emitted from a particular point on the neutron star's surface, every time that point is directly in the line of sight between the pulsar and the observer. That means the time between the emission of each pulse is the same as the time it takes for that point on the star's surface to make one rotation.

What you are implicitly (and incorrectly) claiming is that the time between pulse emissions from the pulsar is the same as the time between pulse receptions at the observer. It's not. The reason why not has already been explicitly stated several times in this thread. I strongly suggest that you go back and read the thread again, carefully, and think carefully about what is going on.

Each rotation of the neutron star is one pulse.

At the star, yes. Not at the observer. See above.

Yet the Relativistic Doppler effect is compacting 20 pulses into the same time interval when travelling at 0.995c towards the neutron star.

This "compression" effect involves something very important other than the time between pulse emissions. Again, what that other something is has been explicitly stated several times in this thread, but you have evidently failed to grasp it. You need to go back and re-read the thread and find it, and take it into account in your analysis.

There is no length contraction any direction perpendicular to the direction of motion

True, but that's only two specific angle values out of a total range of angles of $2 \pi$.

the radius of the neutron star remains the same.

Only at those two specific angle values.

if the axis of rotation from the neutron is parallel to the direction of motion

Where have we assumed that?

then I have something rotating at incredible speeds (with a tangential velocity far greater than 0.6c, which the relativistic vector addition return a tangential velocity with a speed of 0.91c).

A tangential velocity of 0.91 c is still subluminal. I don't know what you mean by "incredible speeds", but you seem to be wandering from the point here.

Perhaps a relativistic form of Cherenkov radiation can resolve this?

This is just unfounded speculation.

 

[King Solomon]

The Doppler effect, I think. I'm not sure what you're trying to say.

Remember that the neutron star is doing 0.995c, right behind the pulses it emits. So the pulses it emits are crowded up when you receive them. That's where the frequency increase comes from.

I understand this part. We could receive nothing other than 20x the number of pulses compared to the initial observation when there no significant motion between the frames.

After watching a few lecture videos on the Relativistic Doppler Effect, this is an absolute fact. I am traveling into a source of emissions that pulsed 100 times per second before I moved, therefore at .995c towards this source they could be nothing other than 2000 times per second.

However, the observed tangential speed, for all velocity vectors perpendicular to my line of sight, was 0.6c. The relativistic addition formula says that we will result with a speed for these tangential vectors of 0.919c, which is in a 1.531666 proportion to 0.6 ; in other words, then it is now rotating 1.53166 times faster, since the radius will remain unchanged (as its axis of rotation was set parallel to the direction of motion).

However, as you said, the neutron star isn't at rest, it's moving at 0.995c towards us. Meaning it gets closer each time a pulse is emitted. I'm going to do a bit more math to see if I can get an individual interval between pulses occurring 1.53155 times faster, with the difference between distances per interval to yield the twentyfold increase of the Doppler.

 

[PeterDonis]

the observed tangential speed, for all velocity vectors perpendicular to my line of sight, was 0.6c.

I'm not sure what you mean by "observed". If you mean it is what the observer will actually see with their eyes or through their telescope, it's not. It is the speed in the pulsar's rest frame.

The relativistic addition formula says that we will result with a speed for these tangential vectors of 0.919c

But these vectors won't be tangential any more in the observer's frame. The pulsar is moving towards the observer, so the spatial motion of the points on its surface in the observer's frame will be at an angle towards the observer.

in other words, then it is now rotating 1.53166 times faster

No, it isn't. The only component of the velocity that is relevant to "rotation" is the component perpendicular to the direction of relative motion. You have to extract that component before you can calculate a rotation rate.

 

[King Solomon]

I'm not sure what you mean by "observed". If you mean it is what the observer will actually see with their eyes or through their telescope, it's not. It is the speed in the pulsar's rest frame.But these vectors won't be tangential any more in the observer's frame. The pulsar is moving towards the observer, so the spatial motion of the points on its surface in the observer's frame will be at an angle towards the observer.No, it isn't. The only component of the velocity that is relevant to "rotation" is the component perpendicular to the direction of relative motion. You have to extract that component before you can calculate a rotation rate.

I see now.

Thus, since equator of the neutron star (whose axis of rotation is parallel to the direction between the observer and the neutron star) is in a plane perpendicular to the observer, the tangential velocity also always remains perpendicular to the observer; thus, the rate of rotation remains the same.

And since the rate of rotation remains the same, the pulses are emitted in the same time intervals; but since the observer is moving towards the neutron star at 0.995c (or vice versa), the observer's motion enacts the Relativistic Doppler Effect; or, if viewed as the Neutron Star moving to the observer; the neutron star emits the pulse, but is also closer to the observer with each pulse; enacting the Relativistic Doppler Effect.

As far the 0.919c speed that is the vector combination of .995c towards the observer and 0.6 perpendicular to the observer, is (as someone said earlier in the thread), the vector that traces a helix; but since all points on the equator move together towards the observer at 0.995c, the result is a cylinder of changing orientation. And thus, the rotation rate for any slice of that cylinder remains 0.6c (as you said, to extract the component).

And therefore the paradox is resolved.

The tangential speed remains 0.6c (which was my original conclusion).

And the number of pulses is twentyfold (not tenfold) like I originally calculated with crude drawings in Microsoft paint.

Isn't this universe amazing?

Thank you.

 

[Vanadium 50]

You are making this way too complicated. The details of emission are irrelevant and all that matters is the Doppler effect.

Imagine you have a pulsar, and a guy next to it turning a flashlight on and off in sync. They must be in sync in every frame, otherwise you could measure absolute velocity by looking at the degree of synchronization. And we know the flashlight is subject to Doppler.

Therefore, the pulsar does the exact same thing.

 

[PeterDonis]

since equator of the neutron star (whose axis of rotation is parallel to the direction between the observer and the neutron star) is in a plane perpendicular to the observer, the tangential velocity also always remains perpendicular to the observer; thus, the rate of rotation remains the same.

No. The correct relativistic velocity addition formula does not say that velocities perpendicular to the direction of relative motion remain the same.

 

[King Solomon]

No. The correct relativistic velocity addition formula does not say that velocities perpendicular to the direction of relative motion remain the same.

Let's change the entire object under consideration. We have a high tech disk with a radius of 10km (like a typical neutron star).

A dim continuous red light is emitted from one node on the circumference, and a dim continuous blue light is emitted rom the opposite end.

As the two nodes rotate about the circumference, each time they reset their original orientation, a green light emits a burst of gamma rays. Also, a power burst of ultraviolent rays are sent from the red nodes, and a powerful burst of x-rays are sent from the blue node.

Since we record 3000 pulses per second, we yield the speed of the tangential vector to be 0.6287c (viz. the linear speed of the red or blue node at any particular instant in time). In doing so, our apparatus is mimicking the behavior of typical millisecond pulsar.

The apparatus is in a plane orthogonal to the observer. Assuming no significant motion between the observer and the disk, we will always receive 3000 pulses per second.

Now the disk moves at 0.995c towards us. The Relativistic Doppler Effect yields a twenty-fold increase in the pulse rate, which is 60,000 pulses per second. So we get blasted with 60,000 gamma bursts per second.

At the same time, we're also being blasted with 60,000 UV bursts from the red node and 60,000 X-ray bursts from the blue node.

Yet there can be no change in the radius of the disk, since it exists in a plane orthogonal to us.

How then do we interpret:
1: The rotation rate of the disk.
2: The tangential speed of the red or blue node at any instance in time?

 

[PeterDonis]

Let's change the entire object under consideration.

I don't see the point of switching scenarios if you haven't even gotten the original one right. The solution of both is the same in any case since we were only concerned with the equatorial plane of the rotating neutron star, which is the same as the rotating disk in your new scenario. So you've already been given the answer to your new scenario anyway.

 

[King Solomon]

I don't see the point of switching scenarios if you haven't even gotten the original one right. The solution of both is the same in any case since we were only concerned with the equatorial plane of the rotating neutron star, which is the same as the rotating disk in your new scenario. So you've already been given the answer to your new scenario anyway.

https://www.astronomy.com/science/weird-object-neutron-star-psr-j1748-2446/

It’s hard to visualize. In everyday life, the fastest-spinning thing we might see is the blade on a kitchen blender or a circular saw. But those never rotate more than a few hundred times a second. This star’s equator moves at one-quarter the speed of light. This rotation of 43,000 miles (70,000km) per second would be like Earth’s equator completing nearly two spins a second instead of one a day.

So now we start moving towards PSR J1748−2446ad at 0.995c, does the 70,000km remain the same or to the speed of light (minus a very small number).

 

[PeterDonis]

So now we start moving towards PSR J1748−2446ad at 0.995c, does the 70,000km remain the same or to the speed of light (minus a very small number).

Neither. Do the math. I've already pointed you at it.

 

[PeterDonis]

the 70,000km

Note that this is a speed in the pulsar's rest frame, and you are asking for a speed in the observer's frame. But this speed is not something the observer directly observes. They have to calculate it. Actually, two ways of making that calculation have been given in this thread. One of them just uses the direct velocity addition formula. The other starts with the Doppler factor, which is directly observed (the pulsar's frequency is 20 times faster) and then corrects for the change in light travel time due to the shortening distance between the pulsar and the observer. The two methods will both give the same answer if done correctly.

 

[Dale]

Closed for mentor discussion

 

[PeterDonis]

After mentor review, this thread will remain closed. The OP scenario has been addressed. Discussion of new scenarios belongs in a new thread. Thanks to all who participated.