Squizzie said:
I'm looking for an explanation which uses standard physics terms and which is consistent with modern scientific theory.
In an attempt to enlighten
@Squizzie, I present here a proof that blast waves always include regions of low pressure. (Inspired by the reasoning used by Penney and Bethe in
https://apps.dtic.mil/sti/tr/pdf/ADA384954.pdf.)
For simplicity, consider the case of a spherically-symmetric explosion into a static atmosphere of uniform density ##\rho_0##. Denote by ##\text{X}## the center of the explosion and draw around it a spherical outer surface of arbitrary radius ##r=R_o##, as shown in the following figure:
Before the explosion, the total mass of atmosphere contained within the outer surface is simply:$$M_{o}^{\text{BE}}=\frac{4\pi}{3}\rho_{0}R_{o}^{3}\tag{1}$$Now trigger the explosion to produce a blast wave (BW), that is, a spherical shell of disturbed atmosphere of fluctuating density ##\rho\left(r\right)##, propagating outward and characterized by a leading and a trailing edge. Focus on the instant that the leading edge of the BW reaches the outer surface, and label the radius of the trailing-edge at that instant to be ##R_i##, as depicted here:
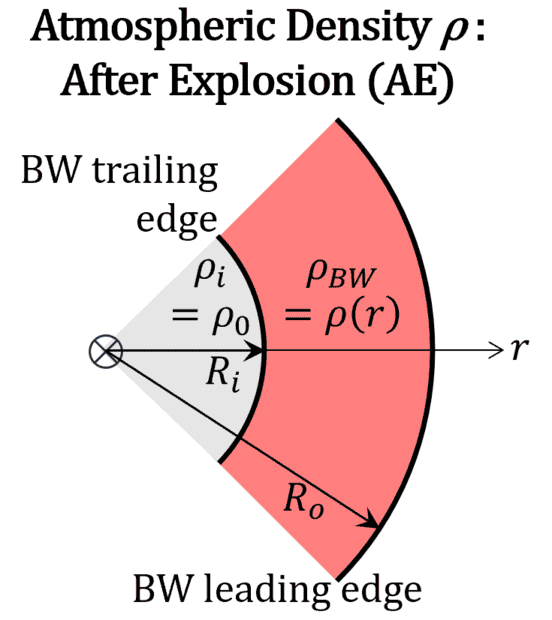
For ##r<R_i##, the atmosphere is undisturbed and has settled back to its prior uniform density ##\rho_0##. (Similarly, for radii larger than ##R_o##, the atmosphere is undisturbed and uniform because the leading edge of the BW has not yet reached there.) In contrast, for the region ##R_i<r<R_o## within the blast wave, the atmospheric density ##\rho\left(r\right)## is unknown without solving a complex problem in fluid dynamics. But even so, after the explosion it's still possible to formally express the the total atmospheric mass within the outer surface as:$$M_{o}^{\text{AE}}=\frac{4\pi}{3}\rho_{0}R_{i}^{3}+4\pi\intop_{R_{i}}^{R_{o}}\rho\left(r\right)r^{2}dr$$$$=\frac{4\pi}{3}\rho_{0}R_{i}^{3}+\frac{4\pi}{3}\overline{\rho}_{\text{BW}}\left(R_{o}^{3}-R_{i}^{3}\right)\tag{2}$$in terms of the average density ##\overline{\rho}_{\text{BW}}## within the blast wave, defined as:$$\overline{\rho}_{\text{BW}}\equiv\frac{\intop_{R_{i}}^{R_{o}}\rho\left(r\right)r^{2}dr}{\frac{1}{3}\left(R_{o}^{3}-R_{i}^{3}\right)}\tag{3}$$Everything to this point is just describing the system and performing some simple math manipulations. But now enters the single fact from physics that is crucial to the proof:
conservation of matter as applied to the atmosphere. That is, both theory and experiment dictates that a disturbance like a blast wave can neither create nor destroy atmospheric material. In particular, this means the total mass of the atmosphere is unchanged by a BW, which says in our notation:$$M_{o}^{\text{BE}}=M_{o}^{\text{AE}}\tag{4}$$Putting eqs.(1), (2) into this gives:$$\frac{4\pi}{3}\rho_{0}R_{o}^{3}=\frac{4\pi}{3}\rho_{0}R_{i}^{3}+\frac{4\pi}{3}\overline{\rho}_{\text{BW}}\left(R_{o}^{3}-R_{i}^{3}\right)$$or more simply:$$\overline{\rho}_{\text{BW}}=\rho_{0}\tag{5}$$In other words, no matter how wildly the density varies inside a blast wave from point to point, the average density is always
exactly the same as that of the undisturbed atmosphere. In particular, maintaining this average within a BW requires that every region of compression (higher density/above atmospheric pressure) must be balanced by one or more regions of rarefaction (lower density/below atmospheric pressure). That's why in an earlier post I drew a comparison to sound waves, where each compression is always followed by rarefaction. All due to conservation of (fluid) matter!