How Is Maximum Speed Calculated for Identical Charges Released Simultaneously?

[apphysicsgirl]

Homework Statement

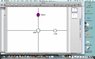
Two identical +6x10^-6 C charges, each with a mass of 10^-6, are placed as shown in the diagram below. All coordinates are in meters.
...
An identical charge is brought in slowly from far away to point P.
...
All three charges are released simultaneously. What is the maximum speed attained by each of them?

Homework Equations

V=U/q
deltaU=-deltaK

The Attempt at a Solution

I found in one part of the question that the work that it took to bring the third charge to point P was 0.18 J. I then did 0.18=-Kf+Ki to try and solve for a velocity. I got 600 m/s, but this was incorrect. I am not sure what else to do; I feel like there is something that I am missing on how to find a velocity for EACH charge.

 

[tramar]

Not exactly sure if this is right, but I would try using:

\Delta K = -q\Delta V

The potential is not the same for all charges, since the distance varies according to:

V=\frac{1}{4\pi\epsilon_o}\frac{q}{r}

For one charge, the total potential is the sum of potentials due to the other two charges.