How is the Answer to 3(d) Found in Simple Harmonic Motion Problem?

AI Thread Summary
The discussion revolves around a simple harmonic motion problem where the calculated velocity at a specific point does not match the answer key. The participant calculated the gradient of the tangent to find the velocity but obtained 0.03 m/s instead of the expected 6 m/s. They used the derivative of the position function but still arrived at a much lower value. The conversation suggests that the answer provided in the book may be incorrect, as the calculations based on the given amplitude and period do not support it. The participant expresses gratitude for the assistance received in clarifying the calculations.
tahmidbro
Messages
15
Reaction score
1
Homework Statement
Simple harmonic motion problem:
How is the answer to 3 (d) is found?
Relevant Equations
N/A
How is the answer to 3 (d) is found?
 

Attachments

  • 232cap.PNG
    232cap.PNG
    41.6 KB · Views: 152
  • vfdsv.PNG
    vfdsv.PNG
    15.7 KB · Views: 165
Physics news on Phys.org
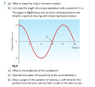
tahmidbro said:
Homework Statement:: Simple harmonic motion problem:
How is the answer to 3 (d) is found?
Relevant Equations:: N/A

How is the answer to 3 (d) is found?
Welcome to PF.

Are you familiar with how to find velocity from a position versus time function?
 
  • Like
Likes etotheipi
Yes. I have drawn a tangent with the curve at 'z' and calculated the gradient.
Gradient = ( 3+3 )/(7-5) = 3 cm/s = 0.03m/s.
But the answer is 6m/s. Will you please tell me how?
 
tahmidbro said:
Yes. I have drawn a tangent with the curve at 'z' and calculated the gradient.
Gradient = ( 3+3 )/(7-5) = 3 cm/s = 0.03m/s.
But the answer is 6m/s. Will you please tell me how?
I have used a derivative to calculate the velocity at that point, and also get a much smaller number than the answer key. If the amplitude is 3cm and the period is 8 seconds, the peak velocity is much less than the 6m/s that is listed as the answer.

Do you know how to do this calculation with a derivative? Also, can you check that answer with the instructor or a teaching assistant?
 
Will you please share your calculation here? are you using v = -Aw sin(wt) ? ( this equation is not in the chapter of the exercise )
well, I am studying by myself. I do not have any instructor or a teaching assistant.
 
tahmidbro said:
Will you please share your calculation here? are you using v = -Aw sin(wt) ? ( this equation is not in the chapter of the exercise )
Yes, good. Differentiating that cos() function does give that derivative.
 
  • Like
Likes tahmidbro
w = 2pi/8 =0.785
A = 3/100 metre . For maximum velocity at 'z', sinwt = 1
v= Aw = 0.785 x 3/100 = 0.0235 m/s
But the answer from the book is 6 m/s. How do I get that?
 
As I said, it looks like the answer provided is wrong. And not by a little bit!
 
  • Like
Likes tahmidbro
berkeman said:
As I said, it looks like the answer provided is wrong. And not by a little bit!
Okay , Thanks for the help!
 
  • Like
Likes berkeman

Similar threads

Solving for Simple Harmonic Motion: A Picture Problem
Replies
1
Views
2K
How to prove that motion is periodic but not simple harmonic?
2
Replies
51
Views
3K
Bungee jump | simple harmonic motion
Replies
5
Views
2K
Position and acceleration in simple harmonic motion given velocity
Replies
16
Views
1K
When Do Sand Particles Slip Off a Vibrating Plate?
Replies
13
Views
1K
Rotating simple harmonic oscillator
Replies
11
Views
1K
Simple Harmonic Motion Experiment Problem
Replies
2
Views
2K
How to know whether motion is simple harmonic motion or not?
Replies
17
Views
2K
Harmonic Motion Problem - Finding oscillation of charges in a circuit
Replies
17
Views
2K
Zero Amplitude Damped Simple Harmonic Motion with k=0.7s^-1 and f=3Hz
Replies
5
Views
1K

Hot Threads

Recent Insights

Back
Top