How Is the Moment Calculated for a Tensioned Cable on a Telephone Pole?

[wilson11]

Homework Statement

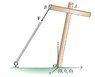
An old wooden telephone pole with a single cross member was blown off center during a recent storm. To temporarily stabilize the telephone pole, a repair crew has attached a cable from the end of the cross member to an eye-ring stake anchored in the ground. (Figure 3) If the origin O of a coordinate system is placed where the pole A(-1.35,-1.25,13.0) meets the ground, the point where the cross member is attached to the pole is and the point where the cable is attached to the end of the cross member is B(-1.35,-1.25,14.5) . The cable's direction is (1.00i,-1.00j,-1.00K) and it has a tension of 925N . What is , the moment that tends to twist the telephone pole due to the tension in the cable applied at point B?

Homework Equations

The Attempt at a Solution

moment= r X T

r is the distance between A and B.

r= position vector of B- position vector of A

=(0, -2.5,1.5)

T=F=925*(1,-1,-1)/√3
= -534.05

This is where i hit a wall and don't know where to go. Please help me :(

 

[voko]

When I compute B - A from your data, I get (0, 0, 1.5), which does not seem right at all. Check your data.

Apart from this, I do not understand what your difficulty is. Given r and F, you just need to do the vector product of them.

 

[wilson11]

I am confused from when i get that answer of 534, what do i do then?
Do I cross product the =(0, -2.5,1.5) with (1-1-1)

I need to find Ma and not sure where to go from here can you please help me?

 

[voko]

When you get 534.05, that means the force is 534.05(1, -1, -1) = (534.05, -534.05, -534.05). You can use either (534.05, -534.05, -534.05) or (1, -1, -1) for the cross-product, just remember you need to multiply the result with 534.05 in the latter case.

 

[wilson11]

so the answer would be the cross product of (534.05,-534.05,-534.05) X (0,-2.5,1.5)?

 

[voko]

As I said, I am not sure about the value of r you got. It does not follow from A and B given.

Next, the vector product depends on the order of the multipliers. What is the correct order?

Finally, once you get the vector product, you need to obtain its magnitude - that's what the question is about.

 

[benzz90]

help...i have this same question and have become very confused?

 

[voko]

What have you done and what confuses you?

 

[benzz90]

i know that i need to use the triple scalar product to determine the moment. However, i am confused on which position vector i would use and how to determine the position vectors length?

If i determine that info i can easily calculate the force components and then then I am again I am confused on how to determine the components of the unit vector that acts along the OA axis.

Once i have determine the all of the above i can simply solve the triple scalar product.

 

[voko]

I do not understand what triple product you need here. You need one vector product to determine the moment.