How is the volume of a parallelepiped with edges A, B, and C calculated?

[tronter]

Homework Statement

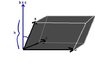
Show that the volume of a parallelepiped with edges A,B,C is given by A \cdot (B \times C).

Homework Equations

The Attempt at a Solution

B \times C is the area of a parallelogram. From here I would I deduce the above result?

 

[tronter]

Is A just the height?

 

[adradmin]

You're right, in two dimensions x and y the area is A=|bxc|. The height is actually |a|*|cos(theta)|. Where theta is the angle between vector a, and the cross product of vectors b and c. I'll include a picture but I hope this helps analytically to prove it. V=|a dot product to (b cross product with c.

 

[adradmin]

https://www.physicsforums.com/attachment.php?attachmentid=11737&stc=1&d=1196123253
parallelepiped.JPG

here is a good diagram for you to visualize... take care