How is this graph Hamiltonian and Eulerian?

[jaus tail]

Homework Statement

Is the graph Hamilton and Eulerian?

Relevant Equations

Hamilton: Path exists that covers all nodes. Starting and Ending node is same. Each node covered only once.
Eulerian: Path exists that covers all paths. Starting and ending node is same. Each path covered only once.

Is the graph Hamilton and Eulerian?

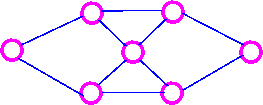
The website says the graph is Hamilton and Eulerian but I think it's wrong.
Ref: https://scanftree.com/Graph-Theory/Eulerian-and-Hamiltonian-Graphs
There is no path that covers all paths only once. Any help? I think the graph is drawn wrongly.

 

[fresh_42]

It is a Hamilton graph, but it is not an Euler graph, since there are 4 knots with an odd degree.
https://en.wikipedia.org/wiki/Eulerian_path

 

[member 587159]

An explicit path that covers all nodes exactly once is for example the following:

Start entirely left, move one right up, one right down, one right up and one rigjt up. Then, you are entirely right. Then move one down, one left, and one left up.

Thus your path is Hamiltonian.

The graph is not Eulerian, and the easiest way to see this is to use the theorem that @fresh_42 used.

 

[epenguin]

It is a Hamilton graph, but it is not an Euler graph, since there are 4 knots with an odd degree.
https://en.wikipedia.org/wiki/Eulerian_path

It is not Eulerian because there is one node with an odd degree.

 

[jaus tail]

Thanks. Guess the website has it wrong then.