beeteep
- 11
- 0
Homework Statement
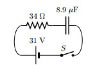
Consider the circuit
How long after the switch is closed does the voltage across the resistor drop to Vf = 20V. Answer in units of s.
Homework Equations
Tc = RC
Q=Qm(1-e-t/RC)
The Attempt at a Solution
[/B]
RC = .0003026
11 = 31(1-e-t/RC)
.3548 = 1-e-t/RC
1.3548 = e-t/RC
ln(1.3548) = -t/RC
.3037*.0003026 = -t
91.886x10-6 s
Answers I've also come to that have been incorrect:
Previous Tries
Try#1: .945
Try#2: .000313554 (using 20 instead of 11 for Q)
Try#3: 91.886e-6