How long does it take to reach 50% of V1?

[Matt Howard]

I'm unsure of the best way to go about finding out the time it takes for the capacitor to reach a voltage of 50% of V1.

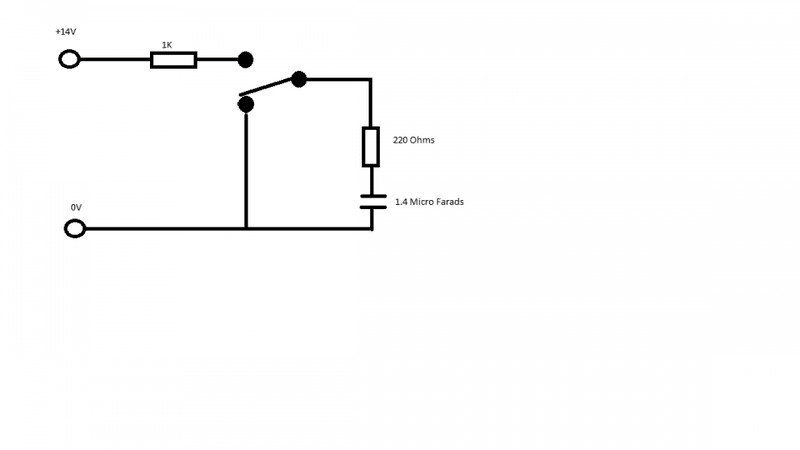
V1: 14V
Resistor before 2pt switch: 1K ohm
Resistor after 2pt switch: 220 ohm
Capacitor: 1.4 micro farads
(Charging) 1 time constant is 1.7mS
(Discharging) 1 time constant is 308 micro seconds

I've attached a picture of the circuit with the values labelled.

Is there an equation for working this out or is there a specific way of working it out? Any help or suggestions are greatly appreciated - I'm not looking for anyone to do the work for me just looking for a jab in the right direction

I thought I could work it out based on the idea that at 1TC the capacitor has reached 63% of the supply voltage (8.82V) and working out the difference there but kept getting myself in a right muddle.

 

[Svein]

You know that charging a capacitor goes according to V=V_{s}(1-e^{\frac{-t}{T}})? And discharging goes as V=V_{0}(e^{\frac{-t}{T}})?

 

[Matt Howard]

I think I vaguely remember that from class. so for me it would be something like: 7=14(1-e^-t/1.7x10-3)? Is that right?
I'm assuming it's t I'm looking for so how would I go about transposing that to solve for t?

 

[SteamKing]

I think I vaguely remember that from class. so for me it would be something like: 7=14(1-e^-t/1.7x10-3)? Is that right?
I'm assuming it's t I'm looking for so how would I go about transposing that to solve for t?

What have you tried?

There's some algebraic simplifications which can be done the equation before solving for t.

 

[Matt Howard]

So simplified is 7=14-14e^-t/1.7x10-3

The only idea I could find (Until Svein commented) was working it out from the fact that the capacitor is 63% charged when 1 time constant had lapsed. I worked out the voltage from that and thought I could work out the time from the differences in percentage and voltage. I.e a very confusing way of doing it that a friend suggested.

 

[psparky]

So simplified is 7=14-14e^-t/1.7x10-3

Yep, that is correct.

Solve for t.

ln .5 = -t/(1.7E-3)

t = 1.18 ms.

 

[psparky]

So simplified is 7=14-14e^-t/1.7x10-3

The only idea I could find (Until Svein commented) was working it out from the fact that the capacitor is 63% charged when 1 time constant had lapsed. I worked out the voltage from that and thought I could work out the time from the differences in percentage and voltage. I.e a very confusing way of doing it that a friend suggested.

This sounds like nonsense. Setting the capacitor voltage to 7 volts in the formula is good. What is said above probably isn't going to do you any favors.
You don't care when it's charged, you just care when it's 7 volts.

 

[NascentOxygen]

The assumption being made is that the switch is moved from its lower position (shown) to its upper position at t=0. Is that what you're told?

I ask only because a different switching scenario is possible.

 

[Matt Howard]

That is correct, the switch is being moved from the lower position to the upper position at t=0

 

[NascentOxygen]

So ... you're all sorted now?

The unfamiliar step was that where you need to take natural logarithms of both sides, in the process losing the exponential function.

 

[Matt Howard]

Yes, I am sorted now, thank you very much! I have now completed the work, thanks again!