How long it takes to discharge capacitor when switch is opened

[Avalanche]

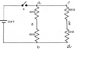
Homework Statement

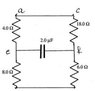
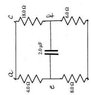
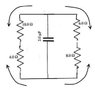
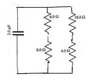
Please look at the attachment. The part I am having problems with is part C

Homework Equations

time constant = RC
Q = Q₀ e^(-t/RC)

The Attempt at a Solution

I don't understand why the circuit is equivalent to the 4 ohm resister with the 18 ohm resistor in series so that the top right loop of the original circuit is now in series

 

[rude man]

You got the right equivalent circuit.

So what is the formula for V(t) on a capacitor intially charged to V_0 and the allowed to discharge thru a resistor R?

(If necessary, write the diff. eq. & solve).

 

[CWatters]

I don't understand why the circuit is equivalent to the 4 ohm resister with the 18 ohm resistor in series

In the following steps I will rearrange the circuit without changing it electrically...

Step 1 Delete components that are not in the circuit when switch is open (eg the battery and some wire).
Step 2 Rotate circuit 90 degrees.
Step 3 Slide the resistors "around the corners"

The 4 and 18 ohm are now clearly in series.

The equivalent resistance is (4+18)//(8+6)

 

[Avalanche]

In the following steps I will rearrange the circuit without changing it electrically...

Step 1 Delete components that are not in the circuit when switch is open (eg the battery and some wire).
Step 2 Rotate circuit 90 degrees.
Step 3 Slide the resistors "around the corners"

The 4 and 18 ohm are now clearly in series.

The equivalent resistance is (4+18)//(8+6)

I think I kind of get it. Why do you have to rearrange the circuit? Is it because you want the resistors to be in parallel with the capacitor?

 

[CWatters]

I think I kind of get it. Why do you have to rearrange the circuit? Is it because you want the resistors to be in parallel with the capacitor?

There is no need to rearrange the circuit - it just makes it more obvious that they are in series when drawn like that (at least it does to me).

It's conventional to draw circuits with the higher voltage nodes at the top of the page and lower voltage nodes at the bottom. (Although in this case I didn't bother to work out which end of the capacitor is the more positive so my redrawn circuit might be upside down). Sometimes redrawing the circuit to comply with this convention can help you understand or recognise what's going on.

It's possible to keep going and redraw it so that voltage sources like the capacitor are on the left and loads like the resistors are on the right...

 

[Avalanche]

I guess my question was why the equivalent resistance wasn't this

 

[CWatters]

The expression "equivalent resistance" comes with the implied "between these two points".

The circuit you posted above would be the way to calculate the equivalent resistance between nodes ac and bd. eg the resistance "seen" by the battery.

The capacitor sees things differently. It's discharging into the equivalent resistance between nodes e and f.