bkraabel
- 26
- 0
Homework Statement
(a) Suppose you have two arrows of equal length on a
tabletop. If you can move them to point in any direction
but they must remain on the tabletop, how many distinct
patterns are possible such that the arrows, treated as vectors,
sum to zero? [Note: If a pattern cannot be rotated on the
tabletop to match another pattern in your list, it is a distinct
pattern.] (b) Repeat part a for three arrows. (c) Repeat for
four arrows. (d) Do you recognize a relationship between
the number of arrows (vectors) and the number of distinct
patterns?
Homework Equations
Sums of x and y components are zero (gives two equations). Magnitudes are all the same (gives n - 1 equations, where n is the number of vectors).
The Attempt at a Solution
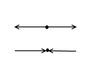
See attachment.
For two vectors, only solution is to have them point in opposite directions.
For three vectors, only solution I can think of is an equilateral triangle.
For four vectors, I can think of three solutions: square, two vectors pointing right and two pointing left, then one right, one left, one right, one left
For five vectors, I can find two solutions: pentagon, pentagon with one adjacent pair of vectors inverted.