AtlBraves
- 11
- 0
I am having trouble with this part of the problem. I set it up like this: -.5*m*v^2 = -.5*k*d^2 so v = sqrt((k*d^2)/m) = sqrt((220*.14^2)/.25) = 4.15 m/s. What am I doing wrong?
A 250 g block is dropped onto a relaxed vertical spring that has a spring constant of k = 2.2 N/cm (Figure 7-42). The block becomes attached to the spring and compresses the spring 14 cm before momentarily stopping.
(c) What is the speed of the block just before it hits the spring? (Assume that friction is negligible.)
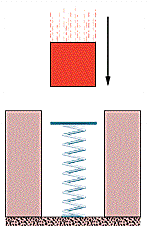
A 250 g block is dropped onto a relaxed vertical spring that has a spring constant of k = 2.2 N/cm (Figure 7-42). The block becomes attached to the spring and compresses the spring 14 cm before momentarily stopping.
(c) What is the speed of the block just before it hits the spring? (Assume that friction is negligible.)