B How to apply Lenz' law if we don't know what to oppose?

[Frigus]

In this question

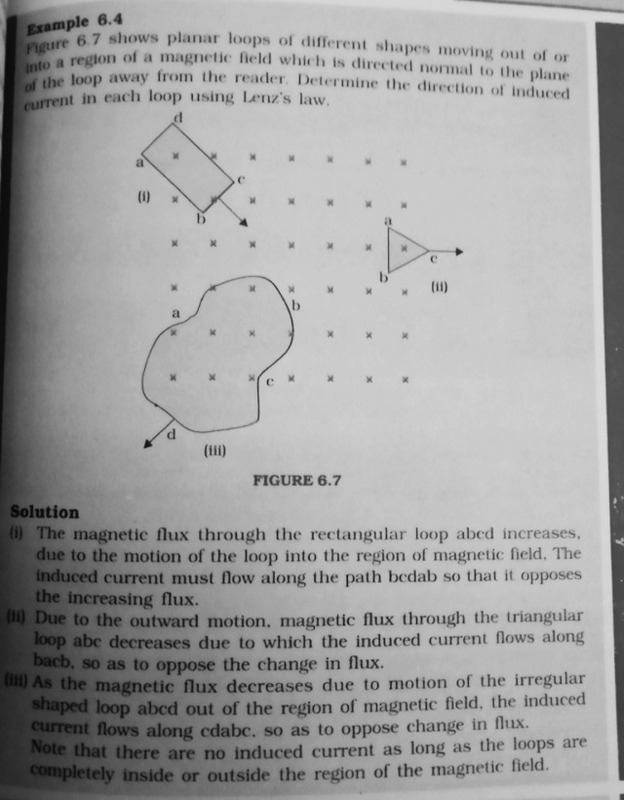
I can't understand how the loop is opposing the change in flux,
I can solve it by simply imagining a bar magnetic with south pole pointing outwards placed inside the plane of image but how do I know that it is the same case as that of bar magnet?
What if their is a case in which the phenomenon is opposed if induced dipole moment is directed along the magnetic field?

 

[Dale]

(1) look at the direction of the flux through the loop (ignore any component of the field across the loop). In this case it is into the loop for all loops.

(2) determine if the field is increasing or decreasing (if it is neither increasing nor decreasing then stop, there is no induced current). For loop (i) it is increasing and for loops (ii) and (iii) it is decreasing.

(3) the change in the flux is in the same direction as the field (step 1) if it is increasing (step 2) or it is in the opposite direction if it is decreasing (step 3). For loop (i) the change in the flux is into the loop and for loops (ii) and (iii) it is out of the loop.

(4) the induced current will produce a field in the direction opposite the change in flux. For loop (i) that is out of the loop and for loops (ii) and (iii) it is into the loop.

(5) use the right hand rule to determine which direction the current needs to flow to produce that field (step 4). For loop (i) that is counter-clockwise and for loops (ii) and (iii) it is clockwise.

 

[Frigus]

(1) look at the direction of the flux through the loop (ignore any component of the field across the loop). In this case it is into the loop for all loops.

Please forgive me if I am going to do some highly stupendous thing,
Isn't flux a directionless quantity?

 

[Dale]

Please forgive me if I am going to do some highly stupendous thing,
Isn't flux a directionless quantity.

No. It is not a vector, so it doesn't have a direction in the meaning of a vector, but it can be positive or negative and so it does have a sense. There is a difference between a positive flux and a negative flux, one representing flux one way through the loop and the other representing flux in the opposite sense.

 

[Frigus]

(1) look at the direction of the flux through the loop (ignore any component of the field across the loop). In this case it is into the loop for all loops.

(2) determine if the field is increasing or decreasing (if it is neither increasing nor decreasing then stop, there is no induced current). For loop (i) it is increasing and for loops (ii) and (iii) it is decreasing.

(3) the change in the flux is in the same direction as the field (step 1) if it is increasing (step 2) or it is in the opposite direction if it is decreasing (step 3). For loop (i) the change in the flux is into the loop and for loops (ii) and (iii) it is out of the loop.

(4) the induced current will produce a field in the direction opposite the change in flux. For loop (i) that is out of the loop and for loops (ii) and (iii) it is into the loop.

(5) use the right hand rule to determine which direction the current needs to flow to produce that field (step 4). For loop (i) that is counter-clockwise and for loops (ii) and (iii) it is clockwise.

Got it.
I think I was just making my life complex.
Thanks for the help.

 

[etotheipi]

I wonder if seeing how to obtain the integral forms of Faraday's law would help you to understand the directions. Take the differential form, $\nabla \times \vec{E} = -\partial_t \vec{B}$, then integrate both sides like$$\int_S (\nabla \times \vec{E}) \cdot d\vec{S} = - \int_S \partial_t \vec{B} \cdot d\vec{S}$$and use Stokes' theorem$$\int_C \vec{E} \cdot d\vec{x} = - \frac{d}{dt} \int_S \vec{B} \cdot d\vec{S} = - \frac{d}{dt} \int_S \vec{B} \cdot \hat{n}dS$$Now $\mathcal{E} = \int \vec{E} \cdot d\vec{x}$ is the EMF, whilst $\Phi = \int \vec{B} \cdot d\vec{S}$ is the magnetic flux. Notice how, like @Dale mentioned, its sign depends on how you choose to orient the vector $d\vec{S}$. The vector $d\vec{x}$ is in a direction given by the right hand rule, with your thumb in the direction of $\hat{n}$. That means that if $\mathcal{E} < 0$, the induced electric field (and by extension, the current) is going the opposite direction to your fingers. And the current loop results in a dipole moment $\vec{\mu} = i\vec{S}$, where again the positive direction of $i$ is consistent with the right hand rule with your thumb along $\vec{S}$.

 

[Frigus]

I wonder if seeing how to obtain the integral forms of Faraday's law would help you to understand the directions. Take the differential form, $\nabla \times \vec{E} = -\partial_t \vec{B}$, then integrate both sides like$$\int_S (\nabla \times \vec{E}) \cdot d\vec{S} = - \int_S \partial_t \vec{B} \cdot d\vec{S}$$and use Stokes' theorem$$\int_C \vec{E} \cdot d\vec{x} = - \frac{d}{dt} \int_S \vec{B} \cdot d\vec{S} = - \frac{d}{dt} \int_S \vec{B} \cdot \hat{n}dS$$Now $\mathcal{E} = \int \vec{E} \cdot d\vec{x}$ is the EMF, whilst $\Phi = \int \vec{B} \cdot d\vec{S}$ is the magnetic flux. Notice how, like @Dale mentioned, its sign depends on how you choose to orient the vector $d\vec{S}$. The vector $d\vec{x}$ is in a direction given by the right hand rule, with your thumb in the direction of $\hat{n}$. That means that if $\mathcal{E} < 0$, the induced electric field (and by extension, the current) is going the opposite direction to your fingers. And the current loop results in a dipole moment $\vec{\mu} = i\vec{S}$, where again the positive direction of $i$ is consistent with the right hand rule with your thumb along $\vec{S}$.

I get stroke by listening to words like strokes theorem ,
These highly fancy things are beyond the scope of our course.

 

[etotheipi]

I get stroke by listening to words like strokes theorem ,
These highly fancy things are beyond the scope of our course.

It's not too fancy, but it is quite neat! It just tells you that, choose any curve $C$ and any surface $S$ which is bounded by that curve. Then the line integral of a vector field around $C$ equals the surface integral of the curl of that same vector field around the surface. That is$$\int_C \vec{F} \cdot d\vec{x} = \int_S (\nabla \times \vec{F}) \cdot d\vec{S}$$You'll notice that the surface integral of any vector field that can be expressed as the curl of another vector field, is the same for all surfaces with the same bounding curve! Since $\vec{B} = \nabla \times \vec{A}$, the magnetic flux depends only on the bounding curve!

 

[Frigus]

It's not too fancy, but it is quite neat! It just tells you that, choose any curve $C$ and any surface $S$ which is bounded by that curve. Then the line integral of a vector field around $C$ equals the surface integral of the curl of that same vector field around the surface. That is$$\int_C \vec{F} \cdot d\vec{x} = \int_S (\nabla \times \vec{F}) \cdot d\vec{S}$$You'll notice that the surface integral of any vector field that can be expressed as the curl of another vector field, is the same for all surfaces with the same bounding curve! Since $\vec{B} = \nabla \times \vec{A}$, the magnetic flux depends only on the bounding curve!

Thanks ethopei,
I tried to understand what you have written and I got a mild sense of what you are trying to make me understand.
I have seen a video about line integral on Khan academy but i didn't worked too hard to understand it as it was out of my course.
Can you please tell me what concepts are required to understand this post so I can watch them on Khan academy to understand.

 

[etotheipi]

If it's not relevant to your course then don't fret too much about it, it's more important to practice the theory you need for your exams.

The classic example for a line integral is work done by a force. Imagine that a particle moves along some trajectory under the influence of a force $\vec{F}$. You could think about calculating the incremental works done by the force over lots of little incremental steps, each of say $\Delta \vec{x}_i$. You would find that$$W = \sum_i \vec{F} \cdot \Delta \vec{x}_i$$The limiting case of such a process is an integral,$$W = \int_C \vec{F} \cdot d\vec{x}$$where $C$ is a curve that represents the trajectory of the particle.

If you do want to learn a bit more, you can try here:
https://tutorial.math.lamar.edu/classes/calciii/calciii.aspx