How to Calculate Equivalent Resistance in a Series-Parallel Circuit

[arl146]

Homework Statement

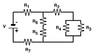
Find the equivalent resistance of the circuit as shown in the diagram below; where R1 = 4.0 , R2 = 3.0 , R3 = 1.0 , R4 = 3.0 , R5 = 2.0 , R6 = 4.0 , and R7 = 1.0 . [Ohm]

Homework Equations

Parallel and series resistance equivalence
Req= 1/R1 + 1/R2 + 1/R3 ... etc
Req= R1 + R2 + R3 etc

The Attempt at a Solution

I said that R3 and R4 are in parallel, R5 and R6 are in series, R2 in series with R34, R345 in parallel with R56, R23456 in series with R7 and the rest in series with R1. What's wrong?

 

[fss]

I don't see any resistor that would be logically be called "R345", for starters.

 

[abe_thebabe]

Find Req R3 and R4 = (1/R3 +1/R4)^-1
Find Req R2 R3 and R4 = (1/R3 +1/R4)^-1 + R2
Find Req R2 R3 R4 R5 R6 = (1/((1/R3 +1/R4)^-1 + R2) + 1/(R5+R6))^-1

Req = (1/((1/R3 +1/R4)^-1 + R2) + 1/(R5+R6))^-1 + R1 + R7

 

[arl146]

Find Req R3 and R4 = (1/R3 +1/R4)^-1
Find Req R2 R3 and R4 = (1/R3 +1/R4)^-1 + R2
Find Req R2 R3 R4 R5 R6 = (1/((1/R3 +1/R4)^-1 + R2) + 1/(R5+R6))^-1

Req = (1/((1/R3 +1/R4)^-1 + R2) + 1/(R5+R6))^-1 + R1 + R7

I'm not really following your Req...

 

[arl146]

I don't see any resistor that would be logically be called "R345", for starters.

Yes, all that means is the sum, whether it be the series or parallel sum (just whatever you used). It's like... the Req of just those 3 resistors. This is the way we learned it in class and it makes a lot of sense.

 

[SammyS]

I don't see any resistor that would be logically be called "R345", for starters.

Hello arl146.

In you Original Post (O.P.), you said:

I said that R3 and R4 are in parallel, R5 and R6 are in series, R2 in series with R34, R345 in parallel with R56, ...

Then you replied to fss:

Yes, all that means is the sum, whether it be the series or parallel sum (just whatever you used). It's like... the Req of just those 3 resistors. This is the way we learned it in class and it makes a lot of sense.

I suspect that fss knew what you meant by R345. However, that appears to be a typo in your O.P. It should say: ... R234 in parallel with R56 ...

- unless somehow R5 is in parallel with itself.

Other than that, your analysis (of what's in series/parallel) looks good to me.

Your equation for the parallel Req is incorrect.

1/Req= 1/R1 + 1/R2 + 1/R3 ... for resistors in parallel.

 

[zgozvrm]

The Attempt at a Solution

I said that R3 and R4 are in parallel, R5 and R6 are in series, R2 in series with R34, R345 in parallel with R56, R23456 in series with R7 and the rest in series with R1. What's wrong?

I get your shorthand. The only problem I see is that R345 should be R245 (the combination of R2 in series with R34, which in turn, is the combination of R3 and R4)

Now, just plug in the numbers and figure out the overall resistance!

 

[arl146]

Yes that's what I meant.. but I did all that and I still can't get it. I don't know what else to do

 

[gneill]

Yes that's what I meant.. but I did all that and I still can't get it. I don't know what else to do

I guess you'll have to lay out your intermediate results, one step at a time, for us to see.

One suggestion I might make, to make your parallel resistance calculations a little cleaner when you're dealing with two parallel resistance at a time, is to use the simplified version of the parallel resistance formula for two resistors:

R1 || R2 = R1*R2/(R1 + R2)

So, show us your calculations and results for R34, R234, ...

 

[arl146]

Okay, so...

R34= 4 those are just added ; R3=1 and R4=3.
R56=4/3 those are in series ; R5*R6/(R5+R6)
R234=12/7 those are in series ; R2*R34/(R2+R34)
R23456=64/21 those are parallel ;
R234567=64/85 those are in series ; (64/21)*(1)/(85/21)
Req= .633663366337 those are in series ; (64/85)*(4)/(4+(64/85))

i found fractions to be easier to put on here but just kept the last a decimal. So any suggestions?

 

[SammyS]

You appear to be using the series expression for parallel & the parallel expression for series.

 

[arl146]

You appear to be using the series expression for parallel & the parallel expression for series.

Wait... I thought parallel was when you just added them? That's what I did right?

 

[gneill]

Resistors in series add as R1 + R2. Resistors in parallel add as R1*R2/(R1 + R2), or, if there's more than two, 1/Rp = 1/R1 + 1/R2 + 1/R3 + ...

Perhaps you were thinking of capacitors?

 

[arl146]

Ohhhh right. I was. Thanks! I'll try that and get back to you :D