SUMMARY
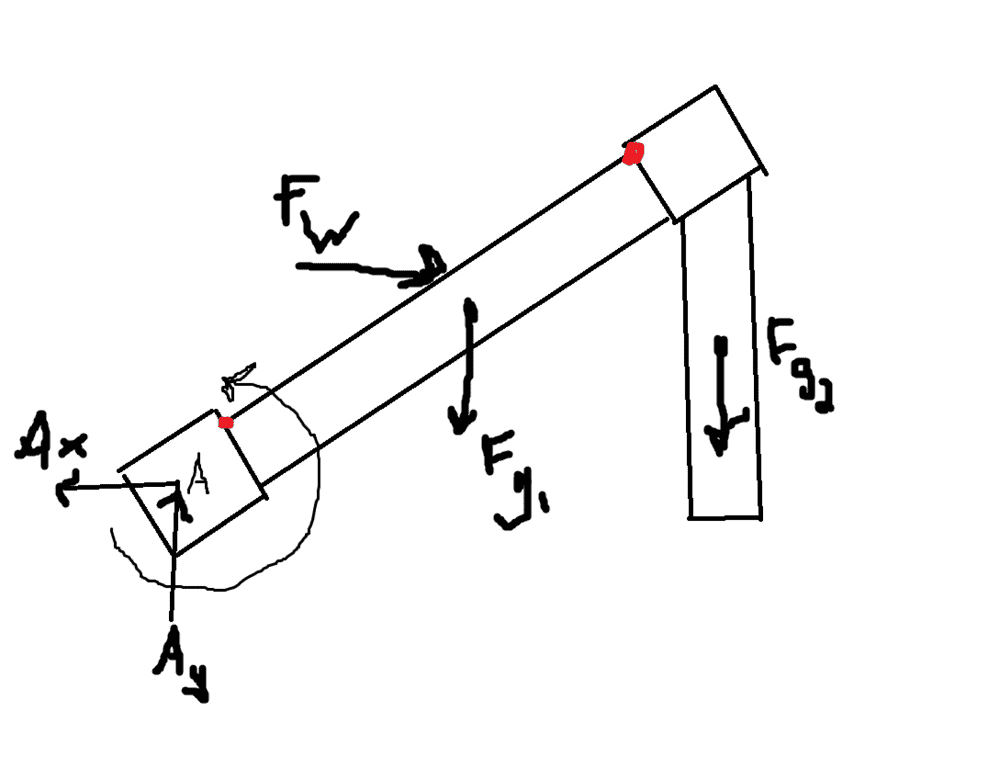
This discussion focuses on calculating failure points in a rigid body subjected to bending moments and external forces, specifically using Finite Element Analysis (FEA) to assess stress concentrations. The conversation highlights the limitations of hand calculations for inclined beams, emphasizing that they cannot accurately predict stress states around sharp corners. Participants agree that von Mises stress must be calculated and compared to the material's yield stress to determine potential failure. Detailed structural information, including size and material properties, is necessary for accurate FEA analysis.
PREREQUISITES
- Understanding of Finite Element Analysis (FEA)
- Knowledge of von Mises stress and yield stress concepts
- Familiarity with shear and bending diagrams
- Basic principles of stress concentrations and notch effects
NEXT STEPS
- Research advanced Finite Element Analysis techniques and software options
- Study the principles of stress concentration factors in mechanical design
- Learn about material properties and their impact on yield stress
- Explore methods for creating high-quality mesh in FEA simulations
USEFUL FOR
Students and professionals in mechanical engineering, particularly those involved in failure analysis, structural design, and stress testing of materials.