How to Calculate Normal Modes in an RLC Circuit with Identical Components?

[Lindsayyyy]

Homework Statement

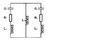
The following circuit is given. C1=C2 L1=L2 R1=R2
I shall calculate the "normal mode" (I'm not sure if this is the 1:1 translation though) of the oscillation

Homework Equations

formula for electrical impedance and differential equations

The Attempt at a Solution

I am very insecure when it comes to curcuits and I have no idea how to handle this correctly. Am I allowed to say that in both circuits is a current flow, which is the same because C1=C2 etc. ?

My attempt was the following:
For both curcuits I have:

(1/c) * I + R * I' + L *I'' = -L12* I''

wheras:
c: capacity
R: electrical resistance
L:inductance
I:current flow and its derivatives


is this the right approach?
If I solve the equation above, is this the normal mode for the whole curcuit because both are the same?

Thank you for your help

 

[Lavabug]

How do you intend to solve the differential equation? Laplace transform? MUC?

 

[Lindsayyyy]

with the approach of

I(t) = I0 * exp(i*w*t)

i: imaginary unit
w: omega
t: time

 

[Lavabug]

That's the actual solution, not the method.

 

[ehild]

For both curcuits I have:

(1/c) * I + R * I' + L *I'' = -L12* I''

wheras:
c: capacity
R: electrical resistance
L:inductance
I:current flow and its derivativesis this the right approach?

It is OK, but a factor of 2 missing on the RHS, if I is the current flowing through a single branch with the capacitor, inductor and resistor. Now assume the solution for I in the form of I=I0 exp(ikt). The real part of k will be the angular frequency.

ehild

 

[Lavabug]

Don't know why you have that term on the right hand side, if you put a 0 there that's the equation for a plain RLC circuit.

Here you've got 2 RLC circuits connected in parallel, along with another inductor in parallel.

What do you know about resistances, inductors and capacitors when wired in parallel? What would the total inductance, resistance and capacitance of the whole circuit be? How would you need to modify the equation of a plain RLC circuit so it works for your problem?

What method are you supposed to use to solve this by the way? Is this from a course on ODE's, integral transforms, plain E&M? There are different ways to solve this. You could just find the roots of the characteristic equation (after calculating your coefficients with the total L, C and R) to get the eigenvalues(frequencies) symbolically, or if you're given initial conditions, use the Laplace transform method.

 

[Lindsayyyy]

That's the actual solution, not the method.

That's our way. I'm not studying pure physics we have differential equations in the 5th semester. I don't like this idea neither, but I don't have much options :(

So I just have to solve one differential equation which gives me the solution? And the algebraic signs are right aswell?

 

[Lavabug]

If this is from an ODE course, I guess the standard course of action is: find the (complex) roots of the characteristic equation and write down the general solution. If no initial conditions are given that's all you can do I think. But the first step is the interesting bit: finding the correct expressions for 1/C, L, and R in the differential equation before solving it. This requires that you know how to add them up when they are connected in parallel.

 

[Lindsayyyy]

parallel? They aren't parallel in this picture or am I mistaken?
So the differential equation I wrote in the first post is right or wrong?

 

[Lavabug]

It would be correct if C, L and R were the totals for that circuit(which isn't necessarily the sum of all of them!). Express C in terms of C1 and C2 when they're parallel, L in terms of L1, L2 when parallel... etc.

 

[Lindsayyyy]

Can you explain me why I shall treat them like they are parallel? I don't understand why I should / why I am allowed to do this.

edit:

My equation would be:

[2/(iwc)] * I +(R/2)*I' + [(iwl)/2]*I'' = -IwL12 * I''

wmega

 

[Lavabug]

Just look at the circuit. Does it look like you have 2 RLC circuits in series? Are your elements connected in the order: R1-L1-C1-R2-L2-C2 ?

R1-L1-C1 is parallel to L12 which is parallel to R2-L2-C2.

 

[Lindsayyyy]

So you mean I have to add up C1, L1 and R1 as they are in series (lets call this sum Z1) and then add Z2 (=C2,L2 and R2) and Z1 like they are parallel?

 

[Lavabug]

No... review your physics, recall how you added resistance etc. for a whole circuit when in parallel...

 

[Lindsayyyy]

I'm confused. 1/Z=(1/Z1)+(1/Z2)

that's what I meant for adding them up, when they are parallel.

 

[vela]

Let Z₁, Z₂, and Z₁₂ be the impedance of the three branches, and I₁, I₂, and I₁₂, the respective currents. The three branches are in parallel, so the voltage V across them will be equal. Ohm's Law gives you:

V = I₁Z₁
V = I₂Z₂
V = I₁₂Z₁₂

Finally, Kirchoff's current law tells you I₁+I₂+I₁₂=0. I didn't work this out, but I think you'll get the original DE you had except for a factor of 2.

Then you can proceed as you said and assume a solution of the form I=I_0e^{i\omega t} and see where it goes from there.

 

[Lindsayyyy]

Thanks everyone for their help, I'll try it tomorrow as I'm tired and have to go to bed soon :)

 

[ehild]

R1-L1-C1 is parallel to L12 which is parallel to R2-L2-C2.

Take care with the terms parallel and series when no source is connected to a circuit. Here the identical branches both are connected (parallel) to the single inductor L12, making a closed loop. The two branches are identical, the current I flowing through both of them is the same and their sum, that is, 2I flows through L12. So Lindsayyyy's equation was correct but a factor of 2 on the right hand side (it should have been -L12*(2I")).

ehild