How to Calculate Tension in a Rope for a Drawbridge with a Rusty Hinge?

[uchicago2012]

Homework Statement

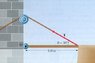
In the figure, the drawbridge has a mass of 800 kg and the hinge is rusty, producing a resistance torque of 10⁴ Nm. What tension in the rope is necessary to raise the bridge?
See Figure 1

Homework Equations

Newton's 2nd law of rotational motion: Torque_net = I * alpha
I = rotational inertia, alpha = rotational acceleration

The Attempt at a Solution

I'm pretty lost on this question. So I said I = (1/2)MR² for the pulley and if I did it correctly I can find the translational acceleration by
Torque_net = I * alpha
(Torque_net = R * f * sin theta, the tension in the cord, T, is tangent to R so theta = 90 and Torque_net = RT)
RT = (1/2)MR² * alpha
T = (1/2)MR * alpha
(alpha = a/R, because the cord doesn't slip. Or it doesn't say it does.)
T = (1/2) Ma

But I'm confused where to go from here because I'm having trouble getting a force diagram for the problem. Should I just assume the center of mass of the drawbridge is in the center? But wouldn't that complicate things, because the cord is pulling on the side of the drawbridge? I also don't know how to equate something to the situation when the "bridge is raised," besides the angle being zero and I haven't figured out a use for the angle yet.

 

[uchicago2012]

Actually, I think I may have been going in the totally wrong direction with that. The hinge is producing the torque and above I calculated T, the tension of the rope, as if the pulley was producing the torque.

Anyone have any ideas how to begin with this problem? I'm out of ideas.