aydos
- 19
- 2
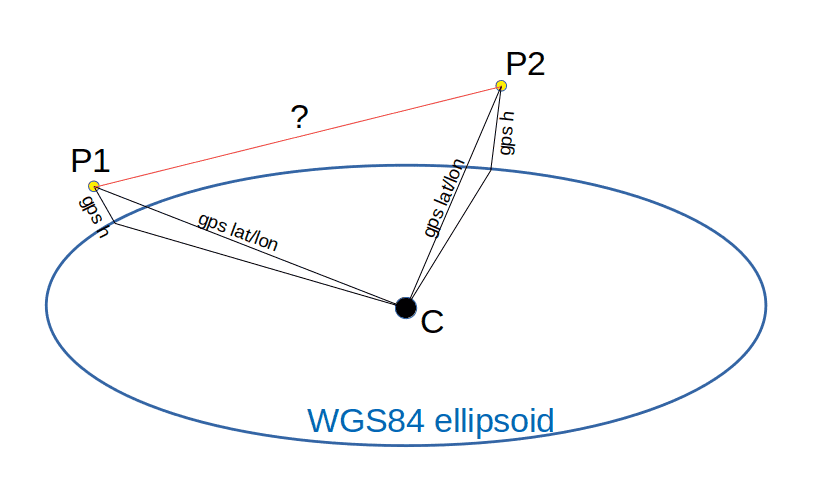
This seems like a trivial question at first, but I am struggling how to get it right. If I have 2 GPS (lat, lon, height) observations P1 and P2 taken at some height from the Earth's surface, how do I calculate the straight line distance between them? I am using the picture below to illustrate the question and get into more detail.
I understand GPS devices provide heights in reference to the WGS84 ellipsoid and perpendicular to the ellipsoid's surface (lines labelled "gps h"). I also understand latitude and longitude are angles originating at the WGS84 ellipsoid centre.
Are my assumptions ok? Can anyone out there can explain how to calculate the distance between P1 and P2?
I understand GPS devices provide heights in reference to the WGS84 ellipsoid and perpendicular to the ellipsoid's surface (lines labelled "gps h"). I also understand latitude and longitude are angles originating at the WGS84 ellipsoid centre.
Are my assumptions ok? Can anyone out there can explain how to calculate the distance between P1 and P2?
