How to Calculate the Area Bounded by y = 2 and y = sec²(3x)?

[shamieh]

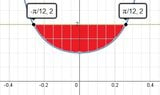
Sketch the region bounded by the line y = 2 and the graph of $$y = sec^2(3x)$$ for $$ \frac{-\pi}{6} < x < \frac{\pi}{6}$$

Very very confused on this problem...

So here is what I set up..

Top function - bottom function

$$\int ^{\pi/6}_{-\pi/6} 2 - \sec^2(3x) dx$$

so I split the integrals in two.

for the first integral, i let u = 3x , du/3 = dx
thus:
$$1/3 \int ^{\pi/6}_{-\pi/6} sec^2(u) du$$

which = $$1/3tan(u)$$ ... Updating the limits $$|^{\pi/2} _ 0$$

here is where I am running into a problem... $$tan(\pi/2)$$ doesn't exist it is infinity or undefined but I'm bounded by y = 2...So why am i running into this problem? If i am bounded then won't i still end up with 2 - infinity? I am confused. Maybe I'm approaching this the wrong way.

 

[MarkFL]

You are asked to find the bounded region, and your limits are within the given interval:

View attachment 2718

You should be able to show your limits are as given in the plot...

 

[Prove It]

You are asked to find the bounded region, and your limits are within the given interval:

View attachment 2718

You should be able to show your limits are as given in the plot...

Are you sure they're not also asking for the area of the regions contained where $\displaystyle \begin{align*} -\frac{\pi}{6} \leq x \leq -\frac{\pi}{12} \end{align*}$ and $\displaystyle \begin{align*} \frac{\pi}{12} \leq x \leq \frac{\pi}{6} \end{align*}$ too Mark?

 

[MarkFL]

Are you sure they're not also asking for the area of the regions contained where $\displaystyle \begin{align*} -\frac{\pi}{6} \leq x \leq -\frac{\pi}{12} \end{align*}$ and $\displaystyle \begin{align*} \frac{\pi}{12} \leq x \leq \frac{\pi}{6} \end{align*}$ too Mark?

I took the restriction $$-\frac{\pi}{6}<x<\frac{\pi}{6}$$ to restrict the problem to one period of the trig. function. :D

 

[shamieh]

You are asked to find the bounded region, and your limits are within the given interval:

View attachment 2718

You should be able to show your limits are as given in the plot...

Sorry I'm not following...Are you saying my limits are incorrect - or that I'm integrating the incorrect way?

 

[MarkFL]

The way I interpreted the problem is that you are to consider the plot of:

$$f(x)=\sec^2(3x)$$

restricted to the interval:

$$\left(-\frac{\pi}{6},\frac{\pi}{6}\right)$$

And then, you are to find the area bounded by this one period of the trigonometric function and the line $y=2$.

 

[shamieh]

The way I interpreted the problem is that you are to consider the plot of:

$$f(x)=\sec^2(3x)$$

restricted to the interval:

$$\left(-\frac{\pi}{6},\frac{\pi}{6}\right)$$

And then, you are to find the area bounded by this one period of the trigonometric function and the line $y=2$.

Oh. I think i see now