How to calculate the force of a charge through its kinetic Energy?

[MichaelC960]

Good Afternoon
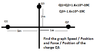
Is it correct to calculate the force of a point charge by relating the force to the kinetic energy and this with its derivative? I have the graphic V/r (Velocity Vs Space), want to calculate force, relate work with force in this way: W=ΔEk, in my case the kinetic energy initial is zero, W=(-1/2)mVo^2.
So W= int(F.ds) ------> ((-1/2)mVo^2)/(ΔS)= F.
I'm not sure about this last step, specifically when deriving (-1/2)mVo^2 = int (F.ds)

Thanks

 

[mfb]

I moved your thread to our homework section.

I’m confused by your notation. What is Vo^2?
Can you post the full original problem statement?

 

[MichaelC960]

Can you post the full original problem statement?

I moved your thread to our homework section.

I’m confused by your notation. What is Vo^2?
Can you post the full original problem statement?

Thank you. And Vo^2 es (Initial Velocity). The problem original it is: https://ibb.co/bwkzy6

 

[mfb]

How did you find the velocity as function of space without calculating the energy or the force first?

The problem statement doesn't say anything about initial speeds, and it doesn't tell us if Q1 and Q2 are fixed (I guess they are).

 

[MichaelC960]

How did you find the velocity as function of space without calculating the energy or the force first?

The problem statement doesn't say anything about initial speeds, and it doesn't tell us if Q1 and Q2 are fixed (I guess they are).

Yes, Q1 and Q2 are fixed. But Q3 is considered as an electron (mass and charge) de Q3.
I calculate the speed as a function of the position using energy conservation, where the initial kinetic energy is zero (starts at rest), and use the electric potential energy U = kQq / r and find the speed as a function of the position.
Sorry for not writing down all the data from the beginning.

 

[mfb]

Finding the force directly or from the potential energy is easier than finding it from the kinetic energy.