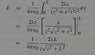You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
How to calculate this integral?
- Thread starter athrun200
- Start date
-
- Tags
- Integral
Physics news on Phys.org
hunt_mat
Homework Helper
- 1,816
- 33
Looks good, what does it come out to?
hunt_mat
Homework Helper
- 1,816
- 33
You're fixing a point z and calculating the electric field there, the limits are easy, you have L=\tan\theta and so the upper limit is \theta =\tan^{-1}L, the lower on is just 0.
Last edited:
athrun200
- 275
- 0
hunt_mat said:You're fixing a point z and calculating the electric field there, the limits are easy, you have L=\tan\theta and so the upper limit is \theta \tan^{-1}L, the lower on is just 0.
Thx!
SammyS
Staff Emeritus
Science Advisor
Homework Helper
- 11,987
- 1,579
For your limits of integration look at your triangle. (The angle you labeled L is actually θ.) If x = 0, then sin θ = 0 and if x = L, then sin θ = L/√(L2+z2) .
Prove $$\int\limits_0^{\sqrt2/4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx = \frac{\pi^2}{8}.$$
Let $$I = \int\limits_0^{\sqrt 2 / 4}\frac{1}{\sqrt{x-x^2}}\arcsin\sqrt{\frac{(x-1)\left(x-1+x\sqrt{9-16x}\right)}{1-2x}} \, \mathrm dx. \tag{1}$$
The representation integral of ##\arcsin## is $$\arcsin u = \int\limits_{0}^{1} \frac{\mathrm dt}{\sqrt{1-t^2}}, \qquad 0 \leqslant u \leqslant 1.$$
Plugging identity above into ##(1)## with ##u...
Similar threads
- Replies
- 5
- Views
- 1K
- Replies
- 2
- Views
- 1K
- Replies
- 6
- Views
- 844
- Replies
- 8
- Views
- 2K
- Replies
- 7
- Views
- 2K
- Replies
- 27
- Views
- 3K
- Replies
- 14
- Views
- 2K
- Replies
- 2
- Views
- 1K
- Replies
- 3
- Views
- 2K
Hot Threads
-
Prove that the integral is equal to ##\pi^2/8##
- Started by Meden Agan
- Replies: 105
- Calculus and Beyond Homework Help
-
Solve this problem that involves induction
- Started by chwala
- Replies: 7
- Calculus and Beyond Homework Help
-
Finding the modulus and argument of ##\dfrac{a}{(b±ci)^n}##
- Started by chwala
- Replies: 17
- Calculus and Beyond Homework Help
Recent Insights
-
Insights Why Entangled Photon-Polarization Qubits Violate Bell’s Inequality
- Started by Greg Bernhardt
- Replies: 26
- Quantum Interpretations and Foundations
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 11
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 7
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 105
- General Math