How to calculate Young's Modulus for flat spring

AI Thread Summary
To calculate Young's modulus for a flat spring, one can apply the principles of cantilever beam deflection. The user initially inquired about the appropriate method for their specific setup, where a force is applied to bend the spring. Chet suggested looking into deflections of cantilever beams, which proved helpful. The user also discovered that Euler–Bernoulli beam theory is relevant for their calculations. Understanding these concepts is essential for accurately determining Young's modulus in this context.
benedict1
Messages
2
Reaction score
0
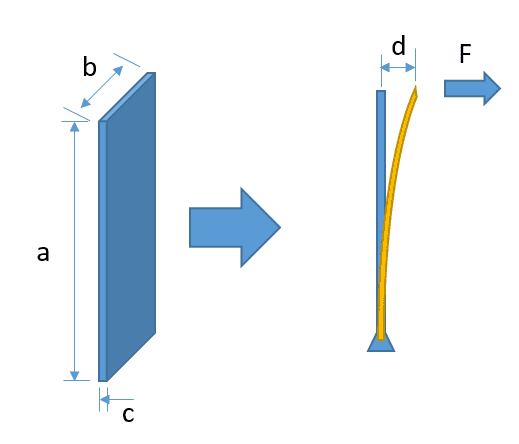
Hi, I have a question regarding calculating Young's modulus for a flat spring. I have a flat spring shown as the left one in the image. Now I fix the bottom of the spring and exert a force F on top of it and it bends for distance of d. Is there any way to calculate young's modulus for this spring? I searched online and found a method called Three point flexural test , but looks different from my case. Thank you.

a.png
 
Physics news on Phys.org
Look up deflections of cantilever beams.

Chet
 
Chestermiller said:
Look up deflections of cantilever beams.

Chet

Thank you Chet, your answer solves my problem. Many thanks.

I also found Euler–Bernoulli beam theory, which is also very useful.
 
Thread 'Is 'Velocity of Transport' a Recognized Term in English Mechanics Literature?'

Thread 'Is 'Velocity of Transport' a Recognized Term in English Mechanics Literature?'

Here are two fragments from Banach's monograph in Mechanics I have never seen the term <<velocity of transport>> in English texts. Actually I have never seen this term being named somehow in English. This term has a name in Russian books. I looked through the original Banach's text in Polish and there is a Polish name for this term. It is a little bit surprising that the Polish name differs from the Russian one and also differs from this English translation. My question is: Is there...
View full post »

Thread 'Is calling fictitious forces "not real" just about terminology?'

Hi there, im studying nanoscience at the university in Basel. Today I looked at the topic of intertial and non-inertial reference frames and the existence of fictitious forces. I understand that you call forces real in physics if they appear in interplay. Meaning that a force is real when there is the "actio" partner to the "reactio" partner. If this condition is not satisfied the force is not real. I also understand that if you specifically look at non-inertial reference frames you can...
View full post »

Similar threads

Calculating Young's Modulus for a Ring Chain of Springs
Replies
19
Views
21K
B Why is Young's modulus constant below the limit of proportionality?
Replies
23
Views
4K
Calculating Young's Modulus from this Stress/Strain Graph
Replies
29
Views
7K
Calculate Frequency of Flat Spring Steel for Reed Valves in a Pulse Jet Engine
Replies
26
Views
5K
Difference Between Young's Modulus & Second Moment of Area
Replies
2
Views
5K
Measuring Tensile Strength in an alternative way
Replies
2
Views
2K
How to calculate energy density of mainspring?
Replies
2
Views
6K
A How to Calculate Young's Modulus for Deformation of a Sphere into an Ellipsoid?
Replies
6
Views
2K
Finding Young’s modulus by bending a beam
Replies
6
Views
12K
How Does Young's Modulus Relate to Spring Constants in Motion Equations?
Replies
3
Views
3K

Hot Threads

Recent Insights

Back
Top