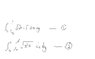The first integral is
\int_{y=0}^1\left[\int_{x= \sqrt{y}}^1 \sqrt{x^2+1}dx\right] dy
and the second is
\int_{x=0}^1\left[\int_{y= 0}^{x^2}\sqrt{x^2+ 1}dy\right] dx
I've included "x= " and "y= " in the limits of the integrals and put in braces, to make it clearer that, in the first line, they are first integrating with respect to x and then with respect to y, while in the second line, they are first integrating with respect to y and then with respect to x. That's signaled in two ways: the first line has "dx dy" while the second line has "dy dx" and the "inner" integral in the first line has a function of y as a limit of integration while the "inner" integral in the second line has a function of x as a limit of integration.
The way to see how to change the limits of integration when changing the order of integration is:
First draw a picture of the region you are integrating over: the "outer" integral in the first line has limits of integration y= 0 and y= 1 (We know they are "y= " because the "outer" integral is with respect to y) so we draw horizontal straight lines at y= 0 and y= 1. The "inner" integral has limits of x= \sqrt{y} and x= 1 so we draw the graphs of x= \sqrt{y} (that's the right half of y= x2) and x= 1 (a vertical line). For each y, (looking at the inner integral again) x goes from \sqrt{y} up to 1 so we are looking at the area to the right of the parabola.
Now "reverse" the order. In order to cover the entire area it should be clear that x must go from 0 to 1. If the "outer" integral is with respect to x, then the limits must be x= 0 up to x= 1. For each x now, y must run from the lower line boundary, y= 0, up to the parabola boundary, y= x2. That gives the limits of integration for the "inner" integral.