girolamo
- 6
- 0
Hello
In every physics book they explain how to compute the force that a spring exert if one of its ends is fixed to a wall (or equivalent) and the other end is compressed or stretched.
But how to deal with the problem if both ends are 'free'.
For example, suppose you have two blocks attached with a spring, and someone apply an horizontal force of, say, 50N. (Lets suppose that there is no friction with the surface, the blocks are originally at rest, the spring is originally in its relaxed state, and the spring constant is, say, 300N/m).
How you would compute the acceleration of each block?
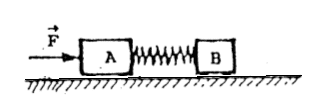
In every physics book they explain how to compute the force that a spring exert if one of its ends is fixed to a wall (or equivalent) and the other end is compressed or stretched.
But how to deal with the problem if both ends are 'free'.
For example, suppose you have two blocks attached with a spring, and someone apply an horizontal force of, say, 50N. (Lets suppose that there is no friction with the surface, the blocks are originally at rest, the spring is originally in its relaxed state, and the spring constant is, say, 300N/m).
How you would compute the acceleration of each block?
Last edited: