How to Derive Thévenin's Equivalent Circuit from Nodes a and b?

[An1MuS]

As seen from a and b.

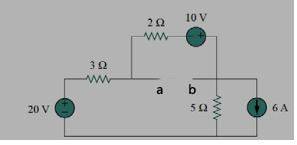
My teacher did the norton's equivalent in the class, and now for studying purposes i was trying to get to the Thévenin's one. However it seems my equations are somehow wrong, and i can't figure out why.

The Eq resistance is 8||2, which is 1.6 ohms.

I tried to apply Nodal analysis first

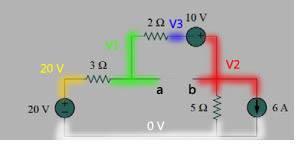
so,
for node V1: \frac{20-V_1}{3}=\frac{V_1-V_3}{2}
for node V2: \frac{V_1-V_3}{2}=6+\frac{V_2-0}{5}=
The relationship between two voltages is also known, which is V_2=V_3+10

which gives V1=2 ; V2=0 ; V3=-10.

V1-V2 should indeed be 2, because from my teachers resolution, Vab = 2V. I don't get is how can V2 be 0? Then there can't be another voltage drop when it reaches the ground (0V)

Also, then i tried mesh analysis:

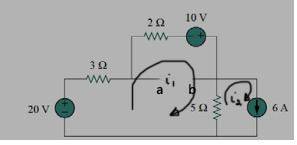
For mesh 120+10=3I_1+2I_1+5(I_1+I_2)
For mesh 2 0=5(I_2-I_1)+v
I_2=6

Where v is the voltage drop across the current source.

It gives I1 = 6 and v (which is equal to the V2 of the nodal analysis) = 0 again.

 

[Jony130]

My answer is that :
V2 is 0V because 6A current source short 5Ω resistor.
Also notice that (20V + 10V) / ( 3Ω + 2Ω ) = 6A

So from superposition point of view we have this situation

V2' = 30*R2/(R1 +R2) = 15V

And

V2'' = - (6A * 5/(10)) * 5 = - 15V

and V2 = V2' + V2'' = 15 + (- 15V) = 0V

 

[An1MuS]

Thanks :) it means the current source is just discharging current. Like i had a current source between two Earth connections.

Another question:

In nodal analysis, when calculating a current entering / leaving a node we do \frac{V_x-V_y}{R} where V_x > V_y My question is: what if we don't know which of the two nodes has higher voltage when writting the equations? Or should it always be possible to know ?

 

[Jony130]

Another question:

In nodal analysis, when calculating a current entering / leaving a node we do \frac{V_x-V_y}{R} where V_x > V_y My question is: what if we don't know which of the two nodes has higher voltage when writting the equations? Or should it always be possible to know ?

You don't need to know which of the two nodes has higher voltage.
All you need to do is assume that one of a voltage nodes has a higher voltage than the other node. And you can treat all nodes individually and assume that the node your currently examining has higher voltage.

For example for this circuit

We can assume Vin > Va > Vout

And we can write nodal equation

\frac{(Vin-Va)}{R1}=\frac{Va}{R3}+\frac{(Va-Vout)}{R2}

\frac{(Va-Vout)}{R2}=\frac{Vout}{R4}

Or we can assume when we examining Va node that Va has the highest voltage.
And this means that all current flow-out (leave) from the Va node.

\frac{(Va-Vin)}{R1}+\frac{Va}{R3}+\frac{(Va-Vout)}{R2} = 0

And the same think we can do for Vout

\frac{(Vout-Va)}{R2}+\frac{Vout}{R4} = 0

Simply I assume that all the current leaving the node. If so this means that the voltage at this node has to be be the highest.

http://www.wolframalpha.com/input/?...+++(A+-+B)/100+=+0+,+B/100+++(B+-+A)/100+=+0+

 

[alphysicist]

Hello,

Thévenin's Equivalent Circuit is a useful concept in circuit analysis that allows us to simplify complex circuits into a single voltage source and a single resistance. It is based on the principle that any linear circuit can be represented by an equivalent circuit with a single voltage source and a single resistance.

In your case, it seems that there may be some errors in your calculations. The equivalent resistance between nodes a and b is indeed 1.6 ohms, as you have correctly calculated. However, your nodal analysis and mesh analysis equations do not seem to be consistent with each other.

In nodal analysis, the voltage at node V2 should be equal to the voltage at node V3 plus 10V, as you have correctly stated. However, in your mesh analysis, you have set the voltage at node V2 to be equal to 0V. This may be the reason for the discrepancy in your results.

I would recommend double-checking your equations and making sure that they are consistent. It may also be helpful to redraw the circuit and label all the nodes and branches to make it easier to track the voltages and currents.

I hope this helps and good luck with your studies! Remember, Thévenin's Equivalent Circuit is a powerful tool in circuit analysis, so keep practicing and you will get the hang of it.